Эффект холла формула: принцип работы, теория, формула, применение — уазмаркет56

Содержание

принцип работы, теория, формула, применение

Принцип эффекта Холла — одна из самых популярных теорий измерения магнитного поля. В этом посте будет обсуждаться эффект Холла: принцип его работы, объяснение теории, формула, применение, включая расчеты для напряжения Холла, коэффициента Холла, концентрации носителей заряда, подвижности Холла и плотности магнитного поля.

Принцип эффекта Холла объясняет поведение носителей заряда при воздействии электрического и магнитного полей. Этот принцип можно рассматривать как расширение силы Лоренца, которая является силой, действующей на носители заряда (электроны и отверстия), проходящие через магнитное поле.

Датчики, работающие по этому принципу, называются датчиками Холла. Эти датчики пользуются большим спросом и имеют очень широкое применение, например, датчики приближения, переключатели, датчики скорости вращения колес, датчики положения и так далее.

История эффекта Холла

Принцип эффекта Холла был назван в честь американского физика Эдвина Холла (1855–1938). Впервые он был представлен миру в 1879 году.

В 1879 году он обнаружил, что когда проводник / полупроводник с током расположен перпендикулярно магнитному полю, генерируется напряжение, которое можно измерить под прямым углом к пути тока. До этого времени электрический ток в проводе считался чем-то похожим на текущую жидкость в трубе.

Принцип эффекта Холла предполагает, что магнитная сила в токе приводит к скученности на конце трубы или провода. Электромагнитный принцип теперь объясняет явления, лежащие в основе эффекта Холла, гораздо лучше. Теория этого ученого, безусловно, намного опередила свое время. Лишь два десятилетия спустя, с введением полупроводников, работы по исследованию эффекта Холла были эффективно использованы.

Первоначально этот принцип использовался для классификации химических образцов. Позднее датчики Холла (с использованием полупроводниковых соединений арсенида индия) стали источником для измерения постоянного или статического магнитного поля без поддержания датчика в движении. Через десятилетие, в 1960-х годах, появились кремниевые полупроводники. Это было время, когда элементы Холла были объединены со встроенными усилителями, и таким образом выключатель Холла был представлен миру.

Принцип работы эффекта Холла

Принцип эффекта Холла гласит, что когда проводник или полупроводник с током, текущим в одном направлении, вводится перпендикулярно магнитному полю, напряжение может быть измерено под прямым углом к пути тока.

Эффект получения измеримого напряжения, как сказано выше, называется эффектом Холла.

Теория за принципом эффекта Холла

Прежде всего мы должны понять, что такое электрический ток. Электрический ток — это в основном поток заряженных частиц через проводящий путь. Эти заряженные частицы могут быть «отрицательно заряженными электронами» или даже «положительно заряженными отверстиями» (пустоты, в которых должны находиться электроны). Теперь давайте перейдем к теме.

Если мы возьмем тонкую проводящую пластину (как показано выше на рис. 1 и повторено ниже для простоты считывания) и подключим ее к цепи с батареей (источником напряжения), то ток начнет течь по ней. Носители заряда будут течь по прямой линии от одного конца пластины к другому.

Поскольку носители заряда находятся в движении, они будут создавать магнитное поле. Теперь, когда вы поместите магнит рядом с пластиной, его магнитное поле будет искажать магнитное поле носителей заряда. Это расстроит прямой поток носителей заряда. Сила, которая нарушает направление потока носителей заряда, называется силой Лоренца.

Из-за искажения в магнитном поле носителей заряда отрицательные заряженные электроны будут отклоняться на одну сторону пластины, а положительные заряженные дыры — на другую сторону. Вот почему разность потенциалов (также называемая напряжением Холла) будет генерироваться между обеими сторонами пластины, что можно измерить с помощью измерителя.

Этот эффект известен как эффект Холла. Чем сильнее магнитное поле, тем больше электронов будет отклоняться. Это означает, что чем выше ток, тем больше электронов будет отклоняться. И чем больше будут отклоняться электроны, тем больше будет разность потенциалов между обеими сторонами пластины. Поэтому мы можем сказать, что:

Напряжение Холла прямо пропорционально электрическому току, и прямо пропорционально приложенному магнитному полю.

Формула эффекта Холла

Вот некоторые математические выражения, которые широко используются в вычислениях эффекта Холла:

Напряжение Холла

Напряжение Холла представлено V _H. Формула для напряжения Холла:

Где:

I — Ток, протекающий через датчик

B — напряженность магнитного поля

q — заряд

n — количество носителей заряда на единицу объема

d — толщина датчика

Коэффициент Холла

Он представлен R_H. Формула для коэффициента Холла: R_H равно 1 / (qn). Коэффициент Холла (R _H) положителен, если число отверстий положительного заряда больше, чем число электронов отрицательного заряда. Аналогично, коэффициент Холла (R_H) отрицателен, если число отрицательных зарядовых электронов больше, чем число отверстий положительного заряда.

Концентрация несущей заряда

Концентрация электронов в носителе заряда обозначена как «n», а «дырки» — как «p». Математическое выражение для концентрации носителей заряда:

Холловская мобильности

Холловская мобильность для электронов представлена как «μ _n», а для отверстий — как «μ _p». Математическое выражение для мобильности Холла:

Где:

μ _n — проводимость за счет электронов

μ _p — проводимость благодаря отверстиям

Плотность магнитного потока

Плотность магнитного потока обозначена буквой «B». Формула для плотности магнитного потока:

Применение принципа эффекта Холла

Принцип эффекта Холла используется в следующих случаях:

Оборудование для измерения магнитного поля.
Множитель приложений для обеспечения фактического умножения.
Тестер эффекта Холла для измерения постоянного тока.
Измерение фазового угла. Например, при измерении углового положения коленчатого вала, чтобы точно выровнять угол зажигания свечей зажигания
Датчики линейных или угловых перемещений. Например, чтобы определить положение автомобильных сидений и ремней безопасности и выступить в роли блокировки для управления подушкой безопасности.
Датчики приближения.
Датчики с эффектом Холла
Для определения скорости вращения колеса и, соответственно, помощи антиблокировочной тормозной системы (ABS).

Как эффект Холла можно использовать для определения типа используемого полупроводника

Коэффициент Холла говорит обо всем. Если коэффициент Холла отрицателен, это означает, что основными носителями заряда являются электроны. И поскольку число электронов больше по сравнению с отверстиями в полупроводниках n-типа, это ясно указывает на то, что испытываемый полупроводник n-типа. Аналогичным образом, если коэффициент Холла положительный, это означает, что основными носителями заряда являются дырки. И поскольку число отверстий больше по сравнению с электронами в полупроводниках p-типа, это ясно указывает на то, что испытываемый полупроводник p-типа.

Эффект Холла и его применение

После проведения эксперимента в 1879 году Эдвином Холлом при пропускании магнитного потока через тонкую пластину из золота было обнаружено возникновение на краях пластины разности потенциалов, то есть образовался эффект Холла.

В чем заключается эффект Холла

Определение 1

При помещении в магнитное поле пластины-проводника или полупроводника под 90 °к направлению силовых линий магнитного потока произойдет перемещение электронов по поперечине пластины под действием силы Лоренца. Их направление зависит от того, в какую сторону идет сила тока и силовые линии магнитного потока. Иначе говоря, (ЭХ) эффект Холла – это частный случай действия силы Лоренца, то есть действия магнитного поля на заряженную частицу.

Это можно рассмотреть на простейшем примере.

Пример 1

Если представить расположенную к нам торцом пластину, то ее кромка направлена вниз. Она сделана из металла, оба торца подключены к источнику питания, задний из которых на минус, передний на плюс.

Данный случай говорит о том, что электрический ток будет протекать по направлению к наблюдателю. Справа и слева от пластины располагаются два магнита. Правый из них обращен к пластине северным полюсом, левый – южным. Делаем вывод, что данный случай показывает направление силовых линий магнитного поля справа налево, так как они всегда выходят из северного полюса и входят в южный. Силовые линии отклоняют электроны, которые проходят по пластине к ее верхней кромке.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

При изменении направления тока в пластине при помощи перемены местами проводников мы сможем наблюдать отклонение электронов вниз. Если направление не менять, а только лишь полюса магнитов, электроны начнут сдвигаться вниз. Когда применяются оба направления, сила Лоренца произведет их перемещение вверх.

Очевидно, что одна из кромок накапливает отрицательный заряд под действием силы Лоренца, на другая на противоположной стороне – положительный. Это говорит о наличии разности потенциалов между ними, то есть электрического напряжения. Увеличение этой разности будет происходить до тех пор, пока не уравновесит силу Лоренца.

Определение 2

Возникновение разности потенциалов в таких случаях, получило название напряжения Холла, которое можно рассчитать, используя формулу:

Uхолл=-IBet, где I является силой тока, B – вектором магнитной индукции, e – зарядом электрона, p – количеством электронов в единице объема, t – толщиной пластины.

Аномальный ЭХ

Имеются случаи, когда ЭХ может быть обнаружен в пластине без пропускания через нее магнитного потока. Это возможно при нарушении симметрии по отношению к обращению времени в системе.

В частности, аномальный ЭХ способен проявляться в намагниченных материалах.

Квантовый ЭХ

Двумерные газы со средним расстоянием между частицами, уменьшенным до значения длины де Бройля на зависимости поперечного сопротивления к воздействию магнитного поля, подвержены возникновению плато сопротивления в поперечине. ЭХ квантуется только в сильных магнитных полях.

Магнитные потоки, обладающие больше силой индукции, имеют дробный квантовый ЭХ. Он взаимосвязан с перестроением внутренней структуры двумерной электронной жидкости.

Спиновый ЭХ

СЭХ можно наблюдать на не намагниченных проводниках, которые не переместили в поле действия силовых линий магнита. Суть эффекта – отклонение электронов с антипараллельными спинами к противоположным краям пластины.

Применение эффекта Холла

Применение метода Холла связано с изучением особенностей полупроводников. С его помощью стало возможным вычисление количества носителей заряда на единицу объема, а также их подвижность. При его использовании реально отличить электрон от квазичастицы с положительным зарядом.

ЭХ всегда считался основой для разработки датчиков Холла. Аппаратура предназначена для измерения напряженности магнитного поля. Их используют для построения моторов со следящим приводом. В моторах они исполняют роль датчика обратной связи. Они способны измерить угол поворота вала мотора.

Датчики Холла устанавливают в электростартерах ДВС, охлаждающих системах ПК, навигационных системах мобильных телефонов, в измерительных приборах для вычисления количества заряда.

Что такое эффект Холла и где он применим?

Американский ученый Эдвин Холл в 1879 году обнаружил, что в помещенном в магнитное поле проводнике возникает разность потенциалов в направлении, перпендикулярном току I и вектору магнитной индукции В. Данный эффект возник вследствие воздействия силы Лоренца на заряды, движущиеся в этом проводнике.

На рисунке ниже изображена тонкая пластина, пронизываемая магнитным полем с индукцией В, направленным перпендикулярно чертежу, причем линии индукции направлены от зрителя и уходят за чертеж (показаны крестиком):

За направление тока I принимают направление движения положительных зарядов, для которых направление вектора скорости V и тока I совпадают (рисунок а)). У зарядов отрицательных векторы тока и скорости направлены в противоположные стороны (рисунок б)). Применив правило левой руки легко убедиться в том, что сила Лоренца в обоих случаях будет направлена к верхней (на рисунке) грани пластины.

Эффект Холла наблюдается у полупроводников и металлов. У полупроводников n – типа, а также у металлов, где носителями зарядов являются электроны, на верхней части пластины будет накапливаться избыточный отрицательный заряд, а нижняя грань будет испытывать недостаток электронов и зарядится положительно, как показано на рисунке ниже (а)):

Результатом этого становится возникновение разницы потенциалов между верхней и нижней гранями проводника U_н.

У полупроводников p – типа, носителями заряда которых являются положительно заряженные дырки, верхняя грань (рисунок выше) приобретает в магнитном поле положительный заряд, а нижняя – отрицательный (рисунок б)). При исследовании распределения зарядов можно определить характер проводимости (электронный или дырочный) полупроводника. Также в процессе изучения эффекта Холла было обнаружено, что некоторые металлы обладают смешанной электронно – дырочной проводимостью. У таких металлов, из — за того, что дырки обладают большей подвижностью, распределение зарядов между верхней и нижней гранями будет такое же, как и у полупроводников p – типа.

Поскольку вектор тока I перпендикулярен скорости V перемещения зарядов и магнитному полю В, то выражение для сила Лоренца будет иметь вид:

Заряды, которые скапливаются на нижней и верхней гранях пластины, создают электрическое поле напряженностью Е, которое будет воздействовать на заряды с силой:

Когда устанавливается стационарное распределение зарядов в поперечном сечении проводника, эти две силы уравновешивают друг друга, то есть F_л = F_эл, поэтому:

Из формулы плотности тока:

Где: q – заряд частицы, n – количество частиц на единицу объема, V – скорость их движения.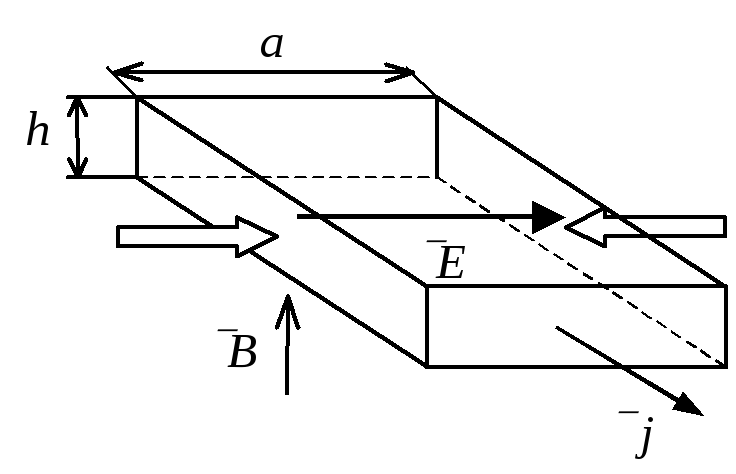

Найдем скорость:

Подставим это выражение в формулу (1):

Разность потенциалов между нижней и верхней гранью с расстоянием между ними d, будет равно:

Коэффициент пропорциональности в этой формуле:

Так же его еще называют постоянной Холла. Уравнение (3) примет вид:

Можно сделать вывод, что разность потенциалов между гранями проводника прямо пропорциональна толщине проводящей пластины d, магнитной индукции В и плотности тока j.

Для любопытных видео о датчиках Холла:

<center><div class="lazy lazy-hidden advv"><ins class="lazy lazy-hidden adsbygoogle" style="display:inline-block;width:336px;height:280px" data-ad-client="ca-pub-1812626643144578" data-ad-slot="9935184599"></ins> <script>(adsbygoogle=window.adsbygoogle||[]).push({});</script></div></center>

Эффект Холла

Описание сути явления

Возникновение разности потенциалов в проводнике с током под воздействием магнитного поля называют эффектом Холла.

Электропроводность металлов зависит от концентрации электронов проводимости (n) и их подвижности (b). Данные величины являются весьма важными характеристиками металла и определяются опытным путем. Так, для измерения концентрации электроном используют эффект Холла. Рассмотрим проводник в виде прямоугольной пластины, в которой течет ток плотности $\overrightarrow{j.}$ Эквипотенциальными поверхностями внутри этой пластины являются плоскости, перпендикулярные направлению тока, следовательно, разность потенциалов на рис.1 между точками (1 и 2) равна нулю.

Рис. 1

Если в металле создать магнитное поле, которое будет перпендикулярно току, то между точками 1 и 2 (рис.1) возникнет разность потенциалов, которая говорит о том, что при наличии магнитного поля эквипотенциальные поверхности в пластинке отклоняются от первоначального положения. В возникновении поперечной разности потенциалов заключается эффект Холла.

Сущность эффекта Холла

Эффект Холла является следствием существования силы Лоренца. На движущиеся в магнитном поле заряды действует сила Лоренца. Под ее действием электрон отклоняется от первоначального направления движения к одной из граней. В результате одна из граней проводника заряжается отрицательно, следовательно, другая становится положительно заряженной. Внутри металла появляется поперечное электрическое поле ($\overrightarrow{E_x}$).

Сущность этого явления заключена в том, что электропроводимость проводника во внешнем магнитном поле является тензорной величиной (не скаляром). Напряженность поперечного электрического поля, которое называют холловским, добавляется к напряженности электрического поля, которое вызывает ток в отсутствии магнитного поля. В результате $\overrightarrow{E}$ поля образует с плотностью тока угол, который называют углом Холла (направление вектора $\overrightarrow{E}$ и направление вектора $\overrightarrow{j\ }\ $ не совпадают). Связь напряжённости и плотности тока имеет вид:

где ${\sigma }_{ik}$ — тензор электропроводимости. Эффект Холла относят к гальваномагнитным эффектам (эффектам, которые происходят в веществе под действие магнитного поля). {-3}.$

Эффект Холла наблюдается не только в металлах, но и например, в полупроводниках. Опыты по изучению эффекта Холла в разных веществах показали, что он не всегда является результатом движения отрицательных зарядов. Если измерение разности потенциалов в эффекте Холла показывает, что движутся положительные заряды, то такой эффект называют аномальным.

Эффект Холла используют создавая так называемые датчики Холла. Они используются для определения параметров магнитных полей, нахождения местоположения объектов.

Данный эффект используют для изучения энергетического спектра носителей заряда в металлах и полупроводниках.

На эффекте Холла основано действие магнитных насосов для стимулирования циркуляции жидких металлов и других проводящих жидкостей и магнитодинамических генераторов энергии.

Для измерения постоянной Холла часто применяют компенсационный метод. Составляют цепь, которая изображена на рис.2. По пластинке А течет ток, к ней подведены два контакта 1 и 2. {-6}В.$

Пример 2

Задание: Получите выражение для постоянной Холла, считая, что проводник с током, помещен в магнитное поле. Следует допустить, что электрон движется равномерно.

Решение:

Сила Лоренца, которая действует на электрон в магнитном поле, движущийся со скорость $\overrightarrow{v}$ равна:

\[\overrightarrow{F}=q_e\overrightarrow{E}+q_e\left[\overrightarrow{v}\overrightarrow{B}\right]\left(2.1\right).\]

В равновесии $\overrightarrow{F}=0$ тогда можно записать, что:

\[q_e\overrightarrow{E}={-q}_e\left[\overrightarrow{v}\overrightarrow{B}\right]\to \overrightarrow{E}=-\left[\overrightarrow{v}\overrightarrow{B}\right]\left(2.2\right).\]

Плотность тока в проводнике можно выразить как:

\[\overrightarrow{j}=-q_en\overrightarrow{v}\left(2.3\right),\]

где $n$ — концентрация электронов. Из $\left(2.3\right)$ выразим скорость:

\[\overrightarrow{v}=-\frac{\overrightarrow{j}}{nq_e}\left(2.4\right).\]

Кроме того разность потенциалов между точками 1- 2 (рис. 1) равна:

\[d\cdot \overrightarrow{E}=U\left(2.5\right).\]

Подставим в (2.5) выражение для напряженности (2.2) и скорость из (2.4), получим:

\[U=d\left[\frac{\overrightarrow{j}}{nq_e}\overrightarrow{B}\right]=\frac{d}{nq_e}\left[\overrightarrow{j}\overrightarrow{B}\right]\left(2.6\right).\]

Выражение для разности потенциалов в эффекте Холла имеет выражение:

\[U=RdjB\left(2.7\right).\]

Получаем, что постоянная Холла равна:

\[R=\frac{1}{nq_e}.\]

Ответ: $R=\frac{1}{nq_e}.$

Эффект холла и датчики на его основе

Эффект Холла.

Эффект Холла относится к группе гальваномагнитных явлений и заключается в том, что под действием магнитного поля, перпендикулярного к электрическому току, электроны в материале отклоняются перпендикулярно как направлению электрического тока, так и магнитного поля. С помощью эффекта Холла стало возможным понять суть процессов проводимости в полупроводниках и провести грань между полупроводниками и другими типами плохо проводящих материалов. Это обусловлено тем, что измерение ЭДС (разности потенциалов) Холла, возникающей в материале перпендикулярно направлению электрического тока и внешнего магнитного поля, дает возможность непосредственно определить концентрацию и знак носителей заряда. Последнее позволяет определить принадлежность материала к тому или иному типу полупроводников (p или n–типа). Измерения эффекта Холла дают возможность отделить случай ионной проводимости от случая электронной проводимости. Наличие эффекта Холла в проводниках и полупроводниках свидетельствует об электронном характере проводимости. С помощью эффекта Холла возможно получить данные и о подвижности носителей заряда (так называемая «холловская» подвижность). Таким образом, можно считать, что эффект Холла – один из наиболее эффективных методов исследования электрических свойств полупроводниковых материалов.

Этот эффект был открыт Е.Холлом в 1879 г.. Сущность явления заключается в следующем. Если металлическую или полупроводниковую пластину, по которой проходит ток, поместить в магнитное поле, направленное перпендикулярно линиям тока (рис. 5), то в ней возникает разность потенциалов в направлении перпендикулярном току и магнитному полю.

В основе эффекта лежит взаимодействие между электрическими зарядами и магнитными полями. Любая заряженная частица, движущаяся в магнитном поле, испытывает действие силы Лоренца, направление которой перпендикулярно направлению движения частицы и направлению магнитного поля. Величина этой силы прямо пропорциональна величине заряда q, скорости частицыv и индукции магнитного поля:

(0.1)

Для металлов и для полупроводников n-типа q = -|e|, где |e|— модуль заряда электрона.

Модуль векторного произведения:

(0.2)

Рис. 5. Схема возникновения эффекта Холла в полупроводнике n-типа.

словимся, что магнитное поле направлено строго перпендикулярно вектору скорости частиц. Т. е. угол α между векторамииравен 900, а sin(900)=1 Тогда:

(1)

Под действием силы Лоренца электроны отклоняются к ближней боковой грани пластины рис.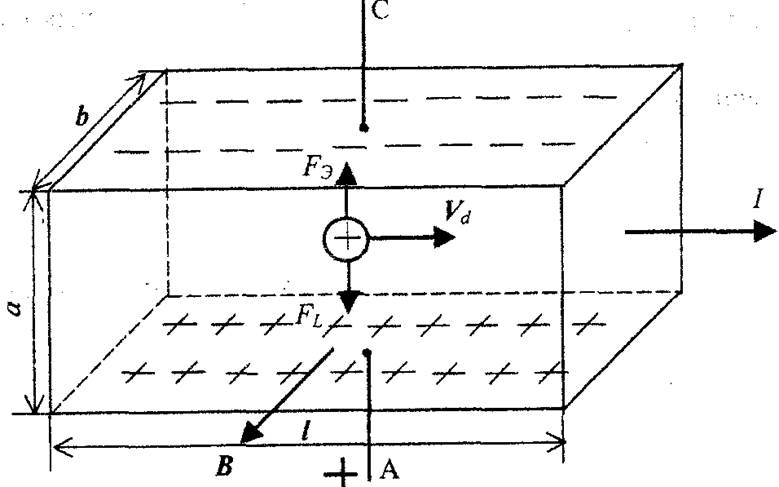 5 и заряжают ее отрицательно. На противоположной грани остается нескомпенсированный положительный заряд ионов кристаллической решетки. В результате этого в пластине возникает поперечное электрическое поле , направленное от дальней боковой грани к ближней. Обозначим напряженность образовавшегося электрического поля через . Сила , действующая со стороны электрического поля на заряд, направлена в сторону, противоположную направлению силы Лоренца (рис. 5). Возникшая вследствие этого поперечная разность потенциалов Ux называется ЭДС Холла.

Разделение зарядов в образце продолжается до тех пор, пока силы магнитного и электрического полей не уравновесят друг друга, т. е.:

(2)

Откуда находим:

(3)

Считаем поле , образовавшееся в пластинке однородным. Тогда находим:

→ (4)

где d – толщина пластинки в направлении поля Ex (рис. 5).

С учетом выражения (3) получаем, что:

(5)

Сила тока, протекающего через единицу поверхности образца, т. е. плотность тока, равна:

(5.1)

А модуль выражения (5.1) найдем как:

(5.2)

где n – число носителей тока в единице объема образца (концентрация носителей тока).

С другой стороны, модуль вектора плотности тока определяется как, где S – площадь поперечного сечения пластины, перпендикулярная направлению. Тогда:

(5.3)

где а— ширина пластины в направлении векторарис. 5.

Сопоставляя формулы (5.2) и (5.3), находим:

(5.4)

Выражая из (5.4) скорость электронов v, находим:

(6)

Подставив (6) в (5), получим:

(7)

Обозначим гдеRх — постоянная или коэффициент Холла. (Условно считают, что знак постоянной Холла совпадает со знаком заряда носителей тока. У электронных полупроводников постояннаяRотрицательна, у дырочных- положительна, гдеp– концентрация дырок).

Тогда выражение (7) записывается в виде:

(8)

Таким образом, ЭДС Холла зависит от величины проходящего тока, индукции магнитного поля, ширины пластины и концентрации носителей заряда. Зависимость от концентрации говорит о том, что в металлах ЭДС Холла по сравнению с полупроводниками намного меньше, и поэтому использование эффекта Холла началось только с применением полупроводников.

При выводе формулы для U мы полагали, что все носители заряда имеют одинаковую скорость. Если учитывать распределение носителей заряда по скоростям, то необходимо ввести числовой множительA,отличный от единицы:

где А– постоянная, зависящая от механизма рассеяния носителей заряда:А=1,93 … 0,99. Практически для большинства металлов можно считать A≈1.

При рассеянии электронов на тепловых колебаниях решетки:

Откуда получаем:

История эффекта Холла

В 1879 году он обнаружил, что когда проводник / полупроводник с током расположен перпендикулярно магнитному полю, генерируется напряжение, которое можно измерить под прямым углом к пути тока. В течение этого времени электрический ток в проводе считался чем-то похожим на текущую жидкость в трубе.

Принцип эффекта Холла предполагает, что магнитная сила в токе приводит к скученности на конце трубы или (провода). Электромагнитный принцип теперь объясняет науку, лежащую в основе эффекта Холла, гораздо лучше. Теория этого зала, безусловно, намного опередила свое время. Лишь два десятилетия спустя, с введением полупроводников, работа и использование эффекта Холла были эффективно использованы.

Первоначально этот принцип использовался для классификации химических образцов. Позднее датчики Холла (с использованием полупроводниковых соединений арсенида индия) стали источником для измерения постоянного или статического магнитного поля, не поддерживая датчик в движении. После десятилетия в 1960-х годах появились кремниевые полупроводники. Это было время, когда элементы Холла были объединены со встроенными усилителями, и таким образом, выключатель Холла был представлен миру.

Теория за принципом эффекта Холла

Прежде всего, мы должны понять, что такое электрический ток. Электрический ток — это в основном поток заряженных частиц через проводящий путь. Эти заряженные частицы могут быть «отрицательно заряженными электронами» или даже «положительно заряженными отверстиями» (пустоты, в которых должны находиться электроны). Теперь давайте перейдем к теме.

Напряжение Холла прямо пропорционально электрическому току, и прямо пропорционально приложенному магнитному полю.

Формула эффекта Холла

Вот некоторые математические выражения, которые широко используются в вычислениях эффекта Холла:

Напряжение Холла

Напряжение Холла представлена V H. Формула для напряжения Холла:

Где:

I — Ток, протекающий через датчик

B — напряженность магнитного поля

q — заряд

n — количество носителей заряда на единицу объема

d — толщина датчика

Коэффициент Холла

Оно представлено RH. Формула для коэффициента Холла (R H ) равно 1 / (qn) . Коэффициент Холла (R H ) положителен, если число отверстий положительного заряда больше, чем число электронов отрицательного заряда. Аналогично, коэффициент Холла (RH) отрицателен, если число отрицательных зарядовых электронов больше, чем число отверстий положительного заряда.

Концентрация несущей заряда

Холловская мобильности

Холловская мобильность для электронов представлена как » μ n «, а для отверстий — как » μ p «. Математическое выражение для мобильности Холла:

Где:

μ n — проводимость за счет электронов

μ p — проводимость благодаря отверстиям

Плотность магнитного потока

Плотность магнитного потока обозначена буквой «B». Формула для плотности магнитного потока:

Эффект Холла

Физика > Эффект Холла

Изучите кратко и понятно определение эффекта Холла. Узнайте, в чем заключается эффект Холла, в чем состоит влияние на заряд в электрическом проводнике, формула.

В момент прохода тока сквозь провод, на который влияет магнитное поле, формируется потенциал, поперечный току.

Задача обучения

Рассмотреть эффект Холла для металла с одним типом носителя заряда.

Основные пункты

Эффект Холла раскрывает явление, где разность напряжений формируется сквозь электрический проводник. Магнитное поле выступает перпендикулярным току.
Транспортировка зарядов в проводе вызовет перемены в траектории, если есть магнитное поле. Поэтому заряды скапливаются на одной стороне материала, а на другой – избыток противоположного заряда. Мы видим электрический потенциал.
Формула для напряжения Холла:

Термины

Элементарный заряд – электрический заряд на одном протоне.
Поперечный – создает угол между пересекающимися предметами.

Давайте кратко и понятно изучим определение эффекта Холла, раскрыв суть явления.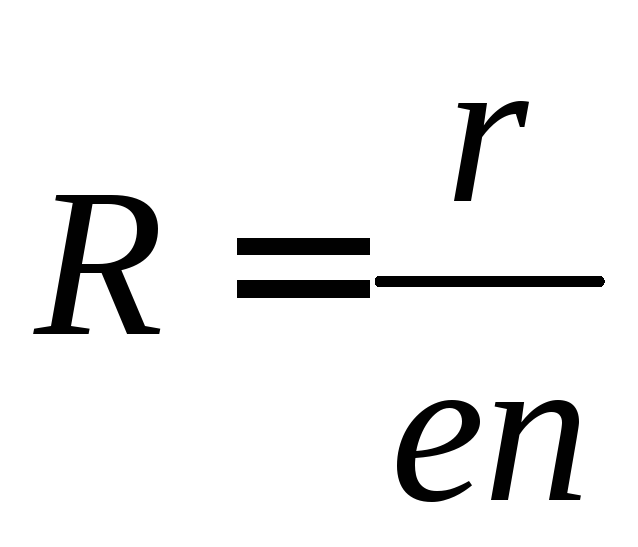 В эффекте Холла отличие напряжений формируется в электрическом проводнике, если есть магнитное поле, перпендикулярное току. При подобной расположенности магнитной силы заряды внутри проводника испытывают силу Лоренца. Если же такое поле отсутствует, то они идут по прямому пути и иногда сталкиваются с примесями.

Перпендикулярная составляющая заставляет путь изгибаться, поэтому заряды скапливаются на одной стороне поверхности материала. На другой возникает тот же избыток, но уже с противоположным знаком. То есть, в потоке заряда создается электрический потенциал. Он вступает в противостояние с магнитной силой и ведет электроны по прямой дороге.

Сначала магнитная сила притягивает электроны и заставляет их продвигаться по изогнутому пути. В итоге, их становится слишком много на левой стороне, а на правой – не достает. Из-за этого формируется электрическое поле. Сила набирает мощность, чтобы компенсировать магнитную, поэтому будущие электроны двигаются прямолинейно

Если вы сталкиваетесь с металлом при едином типе носителя заряда, то значение эффекта рассчитывается, как

(I – коэффициент тока, B – магнитное поле, t – толщина проводящей пластины и n – плотность электронов-носителей).

Коэффициент Холла (R_H) характеризует материал проводника и выясняет соотношение индуцированного электрического поля, плотности тока и магнитного поля:

В физике эффект Холла встречается часто и показывается не только в проводниках, но и среди полупроводников, ионизированных газов и квантовом вращении.

Эффект холла — справочник студента

Узнай стоимость своей работы

Бесплатная оценка заказа!

Эффект Холла наблюдается у полупроводников и металлов. У полупроводников n – типа, а также у металлов, где носителями зарядов являются электроны, на верхней части пластины будет накапливаться избыточный отрицательный заряд, а нижняя грань будет испытывать недостаток электронов и зарядится положительно, как показано на рисунке ниже (а)):
Результатом этого становится возникновение разницы потенциалов между верхней и нижней гранями проводника Uн.

При исследовании распределения зарядов можно определить характер проводимости (электронный или дырочный) полупроводника. Также в процессе изучения эффекта Холла было обнаружено, что некоторые металлы обладают смешанной электронно – дырочной проводимостью.

У таких металлов, из — за того, что дырки обладают большей подвижностью, распределение зарядов между верхней и нижней гранями будет такое же, как и у полупроводников p – типа.

Поскольку вектор тока I перпендикулярен скорости V перемещения зарядов и магнитному полю В, то выражение для сила Лоренца будет иметь вид:
Заряды, которые скапливаются на нижней и верхней гранях пластины, создают электрическое поле напряженностью Е, которое будет воздействовать на заряды с силой:
Когда устанавливается стационарное распределение зарядов в поперечном сечении проводника, эти две силы уравновешивают друг друга, то есть Fл = Fэл, поэтому:
Из формулы плотности тока:
Где: q – заряд частицы, n – количество частиц на единицу объема, V – скорость их движения.
Найдем скорость:
Подставим это выражение в формулу (1):
Разность потенциалов между нижней и верхней гранью с расстоянием между ними d, будет равно:
Коэффициент пропорциональности в этой формуле:
Так же его еще называют постоянной Холла. Уравнение (3) примет вид:
Можно сделать вывод, что разность потенциалов между гранями проводника прямо пропорциональна толщине проводящей пластины d, магнитной индукции В и плотности тока j.
Для любопытных видео о датчиках Холла:

Источник: https://elenergi.ru/effekt-xolla.html

Эффект Холла: в чём заключается явление, измерения датчиками, основанными на элементах Холла, формула расчетов

Открытие эффекта Холла

Первый заключался в том, что силы, возникающие в проводнике, расположенном поперечно линиям магнитной индукции, прикладываются непосредственно к веществу. Второй же сообщал, что значение этих сил зависит от скорости движения зарядов. В 1879 году вышла статья учёного Эдмунда Холла, доказывающая факт, что магнитное поле действует с одинаковым усилием как на подвешенный, так и зафиксированный объект.

Узнай стоимость своей работы

Бесплатная оценка заказа!

Анализируя, какая сила может управлять движением заряженных частиц, он пришёл к выводу, что это может быть только напряжение. Для первого опыта физик использовал согнутую в спираль проволоку зажатую между диэлектриков.

Эту конструкцию он поместил между двумя магнитами и запитал её от химического элемента тока. В качестве регистратора использовался мост Витстона с гальванометром Кельвина. В совокупности было проведено около тринадцати экспериментов и более четырёхсот измерений с разными условиями.

Результатами экспериментов стало утверждение, что магнитный поток может изменять сопротивление материала.

По совету профессора Роуланда было выработано направление нового эксперимента, заключающее в следующем:

К проводящей пластине подводился электрический ток.
Гальванометр подключался к краям проводника.
Включался электромагнит так, чтобы линии напряжённости поля лежали перпендикулярно плоскости пластины.

Предполагалось обнаружить условия для изменения протекания тока. Но опыт не получался, пока в качестве пластины не попробовали использовать тонкий лист из золота. Поставленный новый опыт оказался удачным. Гальванометр чётко зафиксировал появившееся напряжение.

В результате был обнаружено, что при подаче на проводник электрического тока заряд в ней распределяется равномерно по всей её поверхности.

Но как только на пластину воздействует магнитное поле, линии индукции которой перпендикулярны направлению тока, заряд перераспределяется к краям, и возникает разность потенциалов. В этом и заключается эффект Холла, на базе которого были после построены одноимённые датчики.

Физико-математическое определение

Эффект Холла — это явление, которое можно наблюдать при помещении вещества проводящего электрический ток под действие магнитного поля.

Физик Холл открыл, что в проводнике, при пропускании по нему постоянного тока появляется электродвижущая сила (ЭДС) если его поместить в поперечное магнитное поле.

Физически это обозначает возникновение напряжения на боковых гранях проводящего вещества при поднесении к нему магнита.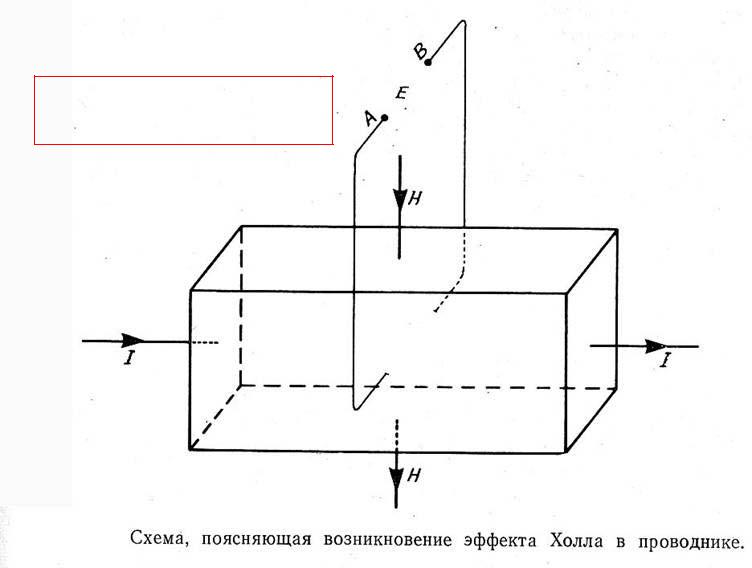 Используя это, можно регистрировать магнитное излучение. Возникшее напряжение зависит от трёх факторов:

силы тока;
напряжённости поля;
типа проводника.

Сила, с которой электромагнитное поле действует на точечный заряд в веществе, называется силой Лоренца. Частным её случаем является сила Ампера. Математически напряжённость электрического поля описывается выражением:

E h = R*H*j*sinα, где:

H — напряжённость магнитного поля;
j — плотность тока;
α — векторный угол между силовыми линиями H и j;
R — постоянная Холла.

Если к пластине прямоугольной формы, имеющую длину L, которая намного будет превышать ширину b и толщину d, подвести ток, то его значение будет определяться формулой: I = j*b*d. Когда же её переместить в магнитное поле, направленное перпендикулярно этому току, то на боковых гранях пластины возникнет ЭДС, равная:

V h = E h* b = R*H*I/d.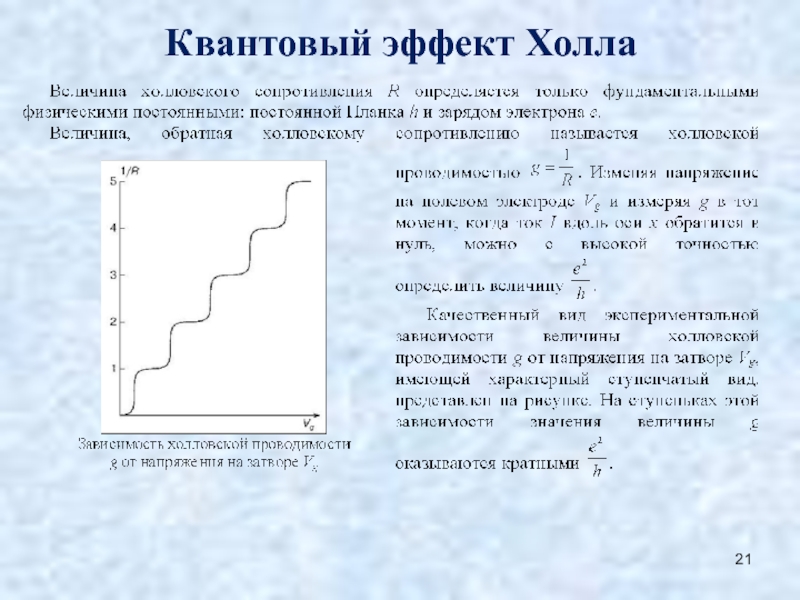

При этом коэффициент Холла равен: R = 1/n*e. Например, для металлов он составляет около 10-3 см3/Кл, а у полупроводников от 10 до 105 см3/Кл.

Постоянную Холла также можно выразить через способность носителей заряда реагировать на внешнее воздействие (подвижность).

Так, она равна: R = µ/σ, где: µ — дрейфовая скорость носителей, а σ — удельная электропроводность. Но это в большей мере справедливо для поликристаллов.

В то же время для анизотропных проводников будет верней формула: R = r/e*n. Здесь r принимается равной единице и обозначает оценку силы магнитного поля.

Разновидности явления

По мере исследования эффекта был обнаружен ряд особенностей появления электрического поля, отличающий от классического понимания. Так, учёными были выявлены факторы, приводящие к появлению напряжения без пропускания через пластинку тока. Такие явления получили название:

аномальное;
квантовое;
спиновое.

Для аномального эффекта необходимым условием является нарушение T-симметрии, то есть уравнений, описывающих физические законы при обращении времени. Наиболее часто этот эффект наблюдается в материалах, имеющих остаточную намагниченность (ферромагнетики).

Квантовое же отклонение возникает в квазидвумерном электронном газе, где пренебрегают кулоновским взаимодействием. В нём носители заряда обладают слабой связью с ионами кристаллической решётки. В такой системе работают законы квантовых теорий.

При этом чем сильнее магнитное поле, тем более выражено дробное явление Холла, связанное с трансформированием структуры всего электронного газа.

В 1971 году учёные Дьяконов и Перель, изучающие механизм спиновой релаксации, обнаружили, что перпендикулярно направлению линий электромагнитного поля наблюдается отклонение носителей зарядов, имеющих противоположные спины. Этот эффект был связан со спин-гальваническим рассеянием и взаимодействием между спиновыми и орбитальными магнитными моментам.

Способы использования явления

На основе эффекта Холла создаются устройства и приборы, обладающие нужными и часто уникальными свойствами. Эти приборы занимают важное место в измерительно-контрольной технике, автоматизации, радиотехнике и т. д. Приспособления, использующие в своей работе явление Холла, называются элементами Холла (датчиками).

Эти датчики дают возможность измерять силу магнитного поля, так как при неизменной величине тока электродвижущая сила прямо пропорциональна линиям магнитной индукции. Прямая зависимость этих величин для элементов Холла является неоспоримым преимуществом перед другими типами измерителей индукции, основанных на контроле магнетосопротивления.

Для этого используется формула эффекта Холла: V h = j*B*H / n*q = B*I / (q*n*α) = R*B*I/α,

из которой число носителей находится как N = (I*B) / (q*α* V h). Таким образом, можно определить не только количество носителей, но и также их тип (знак).

Элементы Холла применяются в автомобилестроении из-за их невысокой стоимости, точности показаний, надёжности и способности не зависеть от условий окружающей среды.

Их используют в конструкции бесконтактных однополярных и биполярных прерывателей.

Благодаря их миниатюрному исполнению электронные гаджеты можно автоматически включать или выключать экран при открытии или закрытии чехла с магнитом. Они помогают в GPS-навигации, улучшая геопозирование.

Источник: https://rusenergetics.ru/praktika/kak-ispolzuetsya-effekt-xolla

Полупроводниковые материалы — Эффект Холла

Page 8 of 8
Ранее были рассмотрены кинетические явления в полупроводниках (перенос свободных носителей заряда) под действием электрического поля, а также при наличии градиента концентрации (градиента температуры).
Гальваномагнитными называют кинетические явления, которые возникают при одновременном действии электрического и магнитного полей.

Если полупроводник (или проводник), вдоль которого течет электрический ток, поместить в магнитное поле, перпендикулярное к направлению тока, то в материале возникает поперечное электрическое поле, перпендикулярное к току и магнитному полю.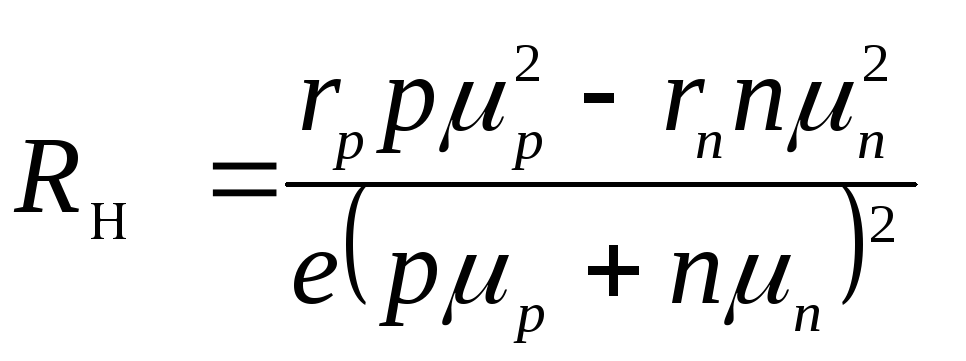 Это явление получило название эффекта Холла, а возникающая поперечная э.д.с. – э.д.с. Холла.

Допустим, что по полупроводнику в виде прямоугольной пластины (рис. 4.17) протекает ток с плотностью

. (4.17)

Рис. 4.17. Образец для измерения э.д.с. Холла

Если полупроводник однородный, то его эквипотенциальные поверхности располагаются перпендикулярно к вектору электрического поля e, следовательно, и к вектору плотности тока j.

С учетом сказанного разность потенциалов между точками А и Б будет равной нулю, так как точки лежат в плоскости, перпендикулярной к вектору j.

При помещении такого полупроводника в магнитное поле напряженностью В, на носитель заряда, дрейфующий со скоростью nдр, будет действовать сила Лоренца

. (4.18)

Если скорость носителей заряда определяется внешним электрическим полем, то направление силы Лоренца не зависит от знака заряда, а определяется только взаимным направлением векторов e и В, т. е.

и электроны, и дырки под действием силы Лоренца отклоняются в одну и ту же сторону.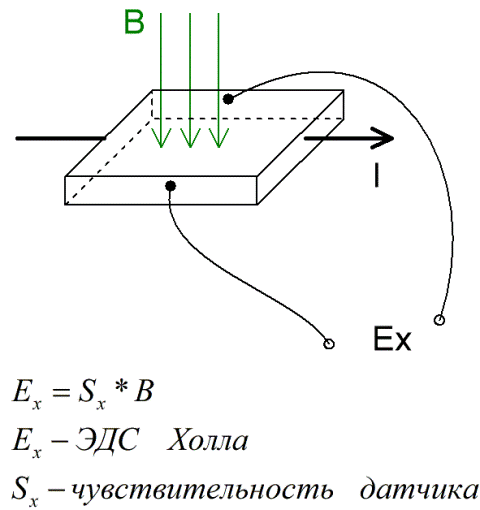

При этом в слабом магнитном поле траектория движения носителей изменяется слабо, а в сильном поле наблюдается значительное искривление траектории.

Для выбранных на рис. 4.18 направлений e и В сила Лоренца действует вверх. Под действием этой силы носители заряда в полупроводнике будут смещаться к верхней поверхности образца.

На нижней поверхности полупроводника возникает дефицит носителей заряда и появляется электрическое поле напряженностью eх, перпендикулярное к направлению внешнего поля e и магнитного поля В. Это явление возникновения поперечной э.д.с.

в полупроводнике с текущим током под действием магнитного поля и называют эффектом Холла. Напряженность поля eх возрастает до тех пор, пока сила, обусловленная этим полем, не скомпенсирует силу Лоренца:

. (4.19)

Если ширину образца принять равной b, то холловская разность потенциалов

. (4.20)

Воспользовавшись выражением (4.17), можно записать

. (4.21)

Рис. 4.18. Отклонение носителей заряда под действием магнитного поля в электронном полупроводнике (а) и в дырочном полупроводнике (б)

Величину Rx принято называть коэффициентом (постоянной) Холла. Для электронных полупроводников
, (4.22)
а для дырочных полупроводников

. (4.23)

Коэффициент Холла обратно пропорционален концентрации основных носителей заряда, а знак его совпадает со знаком этих носителей. Обратно пропорциональная зависимость э.д.с. Холла от концентрации свободных носителей заряда объясняется тем, что при определенной величине тока носители перемещаются тем быстрее и отклоняются магнитным полем тем сильнее, чем меньше их концентрация.

Рассмотренные выше зависимости не учитывают распределения носителей заряда в объеме полупроводника по скоростям. Для учета механизмов рассеяния носителей заряда в полупроводнике вводится холл-фактор r. Тогда для электронного полупроводника коэффициент Холла будет .

При рассеянии на тепловых колебаниях кристаллической решетки r=3p/8, при рассеянии на ионах примеси r=315p/512»1,93. Поскольку рассеяние носителей заряда зависит от температуры, то при определении коэффициента Холла при низких температурах необходимо полагать r=1,93. Для температур, при которых имеет место рассеяние на тепловых колебаниях кристаллической решетки, r=3p/8.

Если в процессе рассеяния одновременно участвуют колебания решетки и ионы примеси, r имеет более сложное выражение.

Произведение |Rx|s имеет размерность подвижности и называется холловской подвижностью носителей заряда mх.

В то же время удельная электропроводность полупроводника, определяемая дрейфовой подвижностью, находится как s=enmдр. Тогда mx=rmдр, то есть холловская подвижность пропорциональна дрейфовой подвижности.

Для металлов и вырожденных полупроводников коэффициент Холла не зависит от механизма рассеяния, поэтому mx=mдр.

Для полупроводников с двумя типами носителей, концентрации и подвижности которых соответственно равны n0, mn и р0, mр, коэффициент Холла

. (4.24)

Для собственного полупроводника n0=p0=ni

, (4.25)

где b=mn/mp. Так как обычно b>1, то в собственных полупроводниках Rx

Источник: http://mashmex.ru/materiali/66-poluprovodnikovie-materiali.html?start=7

Понятие и применение эффекта Холла

Эффект Холла был обнаружен Эдвином Холлом в 1879 году, но прошло много лет, прежде чем технологическое развитие позволило интегральным схемам в полной мере воспользоваться этим явлением. Сегодня микросхемы датчика Холла предлагают удобный способ для достижения точных измерений тока, которые обеспечивают электрическую изоляцию между путем измеряемого тока и измерительной цепью.

От Лоренца к Холлу

Эффект Холла является продолжением силы Лоренца, которая описывает силу, действующую на заряженные частицы – такие как электрон – движущиеся в магнитном поле. Если магнитное поле направлено перпендикулярно направлению движения электронов, на электрон действует сила, которая перпендикулярна и направлению движения, и направлению магнитного поля.

Эффект Холла относится к ситуации, в которой сила Лоренца действует на электроны, движущиеся в проводнике, так что разница потенциалов – или другими словами, напряжение – возникает между двумя сторонами проводника.

Следует отметить, что стрелки на втором рисунке показывают направления протекания обычного тока, а это означает, что электроны двигаются в противоположном направлении. Направление силы Лоренца определяется правилом правой руки, учитывающим направление движения электрона относительно магнитного поля. На первом рисунке электрон движется вправо, а сила Лоренца направлена вверх.

На втором рисунке электроны движутся влево, а сила Лоренца направлена вниз, и, таким образом, отрицательный заряд накапливается на нижней стороне проводника. Результатом является разность потенциалом, которая возникает между верхней и нижней кромками проводника, с верхним краем более положительным по сравнению с нижним.

Эта разность потенциалов называется напряжением Холла:

[U_{Холл}=-frac{IB}{eρt}]

Эта формула, которая применяется к токопроводящей пластине, говорит нам, что напряжение Холла зависит от величины тока (I), протекающего через проводник, от магнитной индукции (B), от элементарного заряда электрона (e), количества электронов в единице объема (ρ) и от толщины пластины (t).

Использование эффекта Холла

Напряжения, генерируемые с помощью эффекта Холла малы по отношению к воздействиям шума, смещения и температуры, которые, как правило, влияют на схему, и, таким образом, реальные датчики на основе эффекта Холла не были широко распространены до появления полупроводниковой технологии, позволившей создание компонентов с высокой степенью интеграции, которые включали в себя и элемент Холла, и дополнительную схему, необходимую для усиления напряжения Холла. Тем не менее, датчики на основе эффекта Холла ограничены в своей способности измерять небольшие токи. Например, чувствительность ACS712 от Allegro MicroSystems составляет 185 мВ/А. Это означает, что ток 10 мА создаст выходное напряжение только 1,85 мВ. Это напряжение может быть приемлемым, если у схемы низкий уровень шума, но, если в цепь протекания тока включить резистор 2 Ом, в результате можно получить напряжение 20 мВ, что значительно лучше.

Эффект Холла используется в различных датчиках; устройства, основанные на относительно простой связи между током, магнитным полем и напряжением, могут использоваться для измерения положения, скорости и напряженности магнитного поля. В данной статье мы сосредоточим внимание на устройствах, которые измеряют ток через напряжение Холла, генерируемое, когда магнитное поле, создаваемое измеряемым током, концентрируется в элементе датчика Холла.

Достоинства и недостатки

Характеристики у разных датчиков тока на основе эффекта Холла сильно отличаются, поэтому трудно суммировать достоинства и недостатки использования эффекта Холла относительно другого распространенного способа измерения тока; а именно, вставки прецизионного резистора в цепь протекания тока и измерения появившегося на нем падения напряжения с помощью дифференциального усилителя. В целом, датчики Холла ценятся за «невлияние» и обеспечение электрической изоляции между цепью протекания тока и измерительной цепью. Эти устройства рассматриваются как не оказывающие влияния потому, что в цепь протекания тока не вставляется какого-либо существенного сопротивления, и, таким образом, схема при проведении измерений ведет себя так же, как если бы датчика не было вовсе. Дополнительным преимуществом является то, что датчиком рассеивается минимальная мощность; это особенно важно при измерении больших токов.

Что касается точности, доступные в настоящее время датчики Холла могут достичь минимальной ошибки в 1%. Хорошо продуманный датчик на основе резистора может дать лучший результат, но одного процента, как правило, хватает при работе с большими токами/напряжениями, где и подходит использование датчиков Холла.

Недостатки датчиков Холла включают в себя ограниченный диапазон частот и высокую стоимость. ACS712 работает до 80 кГц, а диапазон Melexis MLX91208, который позиционируется, как «широкополосный», ограничивается верхней границей 250 кГц.

Резистивный датчик тока с высокоскоростным усилителем, с другой стороны, может хорошо работать и мегагерцовом диапазоне. Кроме того, как обсуждалось выше, эффект Холла по своей природе имеет ограничение в отношении измерения малых токов.

Изоляция

Одно из главных преимуществ датчиков Холла заключается в электрической изоляции, которую в контексте проектирования схем и систем называют гальванической развязкой.

Принцип гальванической развязки используется всякий раз, когда проект требует, чтобы две схемы связывались таким способом, который предотвращает любую возможность протекания между ними электрического тока.

Простой пример, когда цифровой сигнал передается через оптоизолятор, который преобразует импульсы напряжения в импульсы света и таким образом передает данные оптическим способом, а не электрическим. Одной из основных причин для реализации гальванической развязки является предотвращение проблем, связанных с земляными контурами:

Основные принципы проектирования схем предполагают, что взаимосвязанные компоненты совместно используют общую точку земли, на которой предполагается 0 В.

В реальной жизни, однако, «земля» состоит из проводников, имеющих ненулевое сопротивление, и эти проводники служат в качестве обратного пути протекания тока от схемы назад к источнику питания.

Закон Ома напоминает нам, что ток и сопротивление дадут напряжение, и это падение напряжения в обратном пути означает, что «земля» в одной части схемы не точно такая же по потенциалу, как «земля» в другой части схемы. Эта разница в потенциалах земли может привести к проблемам, начиная от незначительных до катастрофических.

Для предотвращения протекания постоянного тока между двумя схемами используется гальваническая развязка, позволяющая успешно общаться схемам с различными потенциалами земли.

Это особенно актуально для измерения токов: низковольтный датчик и обрабатывающая цепь могут понадобиться для контроля больших, изменяющихся в больших пределах токов, например, в цепи привода двигателя.

Эти большие, быстро изменяющиеся токи приведут к значительным колебаниям напряжения в цепи обратного пути протекания тока. Датчик Холла позволяет системе контролировать ток привода и защитить схему высокоточного датчика от этих вредных колебаний земли.

Синфазное напряжение

Другое важное применение датчиков Холла заключается в измерении токов при работе с высокими напряжениями. В схеме резистивного датчика тока дифференциальный усилитель измеряет разницу между напряжениями на одной стороне резистора и на другой. Проблема возникает, когда эти напряжения велики по сравнению с потенциалом земли:

Реальные усилители имеют ограниченный «диапазон синфазности», что означает, что устройство не будет функционировать должным образом, разница между входными напряжениями мала, и очень велика разница между ними и землей.

Диапазоны синфазных входных напряжений токоизмерительных усилителей, как правило, не выходят за пределы 80 или 100 В. С другой стороны, датчики Холла могут преобразовать ток в напряжение без связи с потенциалом земли в измеряемой цепи.

Следовательно, пока напряжение не достаточно велико, чтобы вызвать физическое повреждение, синфазное напряжение не влияет на работу датчика Холла.

Оригинал статьи

Robert Keim. Understanding and Applying the Hall Effect

Применение эффекта Холла

С.А. МАНЕГО, Ю.А. БУМАЙ, В.В. ЧЕРНЫЙ

ЭФФЕКТ ХОЛЛА
Рекомендовано УМО по образованию в области приборостроения в качестве учебно-методического пособия для студентов специальностей
1-38 02 01Информационно-измерительная техника
1-38 02 03Техническое обеспечение безопасности
Минск
БНТУ
УДК 537,633,2 (075.8)
ББК 22.334я7
М23
Составители:

С.А. Манего, Ю.А. Бумай, В.В. Черный

Рецензенты:

Кафедра физики полупроводников и наноэлектроники БГУ, С.Н. Собчук

М 23 Эффект Холла /сост. С.А. Манего, Ю.А. Бумай, В.В. Черный. ‒ Минск: БНТУ, 2014. 22 с.

Учебно-методическое пособие содержит в краткой форме теорию важнейшего из гальваномагнитных эффектов – эффекта Холла. Рассмотрены практические применения эффекта.

Приведена также схема экспериментальной установки для исследования эффекта Холла.

Показано, как на основании экспериментальных данных определяются важнейшие характеристики полупроводника – концентрация носителей заряда и их подвижность.

Учебно-методическое пособие предназначено для студентов инженерных специальностей, изучающих раздел “ Электричество и магнетизм ” курса общей физики.
УДК 537,633,2 (075.8)
ББК 22.334я7
© БНТУ, 2014

ЭФФЕКТ ХОЛЛА

Цели работы:

1. Изучить теоретические основы эффекта Холла.

2. Изучить связь параметров материалов с результатами измерений эффекта Холла.

Задачи работы:

1. Провести электрические измерения и измерения эффекта Холла.

2. Определить концентрацию и подвижность носителей тока в полупроводнике.

Гальваномагнитные эффекты

Физические явления, обусловленные движением носителей заряда под действием внешних и внутренних полей или разности температур, называются кинетическими явлениямиили явлениями переноса.

К ним относятся электропроводность и теплопроводность, гальваномагнитные, термомагнитные и термоэлектрические явления. Кинетические явления лежат в основе фотоэлектрических и фотомагнитных эффектов.

Среди многообразия кинетических эффектов под названием гальваномагнитных объединяются эффекты, возникающие в веществе, находящемся в магнитном поле, при прохождении через вещество электрического тока под действием электрического поля.

Другими словами, гальваномагнитные явления наблюдаются в веществе при совместном действии электрического и магнитного полей. К важнейшим гальваномагнитным явлениямотносятся:

1. эффект Холла;

2. магниторезистивный эффект или магнетосопротивление;

3. эффект Эттингсгаузена, или поперечный гальваномагнитный эффект;

4. эффект Нернста, или продольный гальваномагнитный эффект.

Эффекты перечислены в порядке их практической значимости. Названия «продольный» и «поперечный» отражают направление градиентов температуры относительно тока. Рассмотрим эти эффекты

Эффект Холла

Американский физик Эдвин Герберт Холл в 1879 году впервые описал явление, впоследствии названное его именем.

Явление, открытое Холлом, состоит в том, что в проводнике с током, помещенном в магнитное поле, перпендикулярное направлению тока, возникает электрическое поле в направлении, перпендикулярном направлениям тока и магнитного поля.

Наиболее важным применением эффекта Холла является определение концентрации носителей зарядав материалах, проводящих электрический ток, в частности, в полупроводниках, у которых концентрацию носителей зарядов можно произвольно изменить, например, за счет введения примесей.

Обратимся к чисто примесному полупроводнику, для определенности электронному. Схема, иллюстрирующая возникновение эффекта Холла, изображена на рисунке 1.

К образцу прямоугольной формы, расположенному по длине вдоль оси Х, приложено электрическое поле Е, вызывающее электрический ток плотностью:
Jx = –enVx = σEx, (1),
где: e – абсолютная величина заряда электрона; n – собственная концентрация электронов в объеме полупроводника.
Образец помещен в магнитное поле В, параллельно оси Z. В результате действия на движущиеся носители силы Лоренца
F= –e[V,B] (2)

электроны отклоняются в отрицательном направлении оси Y(дрейфовая скорость электронов Vнаправлена против тока) и скапливаются у боковой (передней) грани образца. Их накопление идет до тех пор, пока поперечное электрическое поле (поле Холла) не компенсирует поле силы Лоренца в направлении оси Y.

Вследствие появления поперечного поля Холла Ерезультирующее электрическое поле в образце конечных размеров будет повернуто относительно оси Х на некоторый угол φн (угол Холла), а ток будет идти лишь в направлении оси Х. Как видно из рисунка 1, угол определяется при этом соотношением:

где μ – дрейфовая подвижность.

Поскольку поле Холла Еy уравновешивает силу Лоренца, можно полагать, что оно должно быть пропорционально как приложенному полю В, так и току Jx в полупроводнике. Поэтому величину, называемую коэффициентом Холла, определяют так:

Следует обратить внимание на то, что, поскольку поле Холла направленно против оси Y (рис. 1), коэффициент R должен быть отрицательным.

С другой стороны, если бы заряд носителей был положительным (в дырочном полупроводнике), знак их Х-компоненты скорости был бы обратным, и сила Лоренца осталась бы по направлению неизменной. В результате поле Холла, имело бы направление, противоположное тому, которое оно имеет при отрицательно заряженных носителях.

Из этого вывода следует, что по знаку ЭДС Холла можно определить знак носителей заряда и,следовательно, тип проводимости полупроводника.
Чтобы рассчитать коэффициент Холла, воспользуемся выражением для общей силы, действующей на электрон со стороны электрического и магнитного полей. В общем случае эта сила определяется векторным уравнением:
F= –еЕ– e[V,B]. (5)

Рис. 1. Схема возникновения эффекта Холла при действии силы Лоренца на движущиеся электроны.

Величина холловского поля определяется балансом сил в направлении оси Y, при котором F= 0. Отсюда:
Еy = –VxB. (6
Тогда, воспользовавшись соотношением (1), имеем:

Сравнивая (4) и (7), видим, что:

Таким образом, коэффициент Холла обратно пропорционален концентрации носителейи ни от каких других параметров полупроводника не зависит. Знак «минус» показывает электронную проводимость, дырочной проводимости соответствует знак «плюс».

Для практического определения коэффициента Холла воспользуемся уравнением (7), заменив напряженность электрического поля Ey потенциалом поля.

В случае однородного образца мы имеем:

где Ux – холловская разность потенциалов или э.д.с.Холла. С учетом выражений (7) и (10) э.д.с. Холла равна:

где: — a и b поперечные размеры образца, a, b(соответственно по направлениям z и y); Ix – сила тока, протекающая через образец; Bz – индукция магнитного поля.
В действительности произведенный элементарный вывод коэффициента Холла не точен: в нем предполагалось, что все носители имеют одинаковую дрейфовую скорость, и не учитывался характер распределения электронов по скоростям и механизм рассеяния носителей.
Более строгое выражение для коэффициента Холла имеет вид:
(12),

где r = /2, r – называют холл-фактором, τ – время релаксации носителей заряда. Через n в данном случае обозначена концентрация носителей (электронов или дырок). Параметр r является атрибутом реального твердого тела и зависит от механизма рассеяния носителей.

Так, — при рассеянии на ионах примеси r = 315π/512 = 1,93, что обычно имеет место в области низких температур;
— при рассеянии на тепловых колебаниях решетки r = 3π/8 = 1,18 — соответствует более высокой области температур;
— при рассеянии на нейтральных примесях, а также в металлах и сильно вырожденных полупроводниках r = 1.
В полупроводнике со смешанной проводимостью в слабом магнитном поле ( ) коэффициент Холла равен
(13)
Так как в случае собственной проводимости n = p = ni, то, введя b = μn / μp, для собственного полупроводника, получим:
, (14)

т. е. знак Rн определяется тем типом носителей тока, подвижность которых больше. Обычно отношение дрейфовых подвижностей b > 1 и R n = p и μn = μp), коэффициент Холла, а следовательно, и ЭДС Холла равны нулю.

Из формулы (13) следует, что для получения максимальных значений RH целесообразно использовать полупроводник с одним знаком носителей заряда. В этом случае (13) переходит в (12) и ЭДС Холла максимальна.

Рассмотрим теперь произведение коэффициента Холла Rн и электропроводности σ = enμ для чисто примесного полупроводника. С учетом (12)
(15)
Мы видим, что величина |Rн|σ пропорциональна величине дрейфовой подвижности μ, при этом коэффициентом пропорциональности является безразмерная константа r (холл-фактор). Поэтому величина
μn=|Rн|σ (16)
имеет размерность подвижности и называется холловской подвижностью.

Таким образом, определив экспериментально Rн, σ и взяв их произведение, получим μn. Если известен механизм рассеяния, то по μn можно определить дрейфовую подвижность μ = μn/r, а по Rн – концентрацию носителей заряда и их знак; благодаря этому эффект Холла является одним из важнейших методов исследования полупроводника.

Выражение для практического определения коэффициента Холла можно получить из формулы (11):
(17)
В системе СИ Rx имеет размерность м3/Кл. Тогда из формулы (12) можно найти концентрацию носителей заряда
(18)
(19)

Одновременно с постоянной Холла определяют удельную проводимость образца «σ». Для образца с данными размерами (рис.2) удельная проводимость определяется по формуле:

(20)
Так как
(21)
(22)
Отсюда, можно определить подвижность электронов и дырок:
(23)
(24)
Применение эффекта Холла

На основе эффекта Холла можно создать ряд устройств и приборов, обладающих ценными и даже уникальными свойствами и занимающих важное место в измерительной технике, автоматике, радиотехнике и т. д. Приборы, созданные на основе эффекта Холла, называют датчиками Холла.

Датчики Холла позволяют измерять величину магнитного поля. Как видно из (11), при постоянной величине тока Э.Д.С. Холла прямо пропорциональна магнитной индукции. Линейная зависимость этих величин для датчиков Холла является преимуществом перед измерителями индукции на основе магнетосопротивления.

Датчики Холла также позволяют измерять электрические и магнитные характеристики металлов и полупроводников. В настоящее время в силу высокой точности, постоянства данных, надежности они нашли широкое применение в различных отраслях науки и техники.

Датчики Холла могут применяться для измерения силы, давлений, углов, перемещений и других неэлектрических величин. При производстве полупроводниковых материалов эффект Холла используется для измерения подвижности и концентрации носителей в них. Для этой цели на специальном подготовленном образце измеряют э. д. с.

Холла и по его величине судят о подвижности и концентрации носителей заряда материала, используемого для изготовления полупроводниковых приборов.

Датчики Холла используются в автомобилях, из-за их низкой стоимости, качества, надежности и способности противостоять жестким условиям окружающей среды. Датчики Холла используют в создании бесконтактных однополярных и биполярных выключателей и переключателей. Основные преимущества датчиков Холла — бесконтактность, отсутствие любых механических нагрузок и загрязнений.

Рекомендуемые страницы:

Источник: https://poisk-ru.ru/s10870t3.html

Эффект Холла: принцип работы, теория, формула, применение

История эффекта Холла

Принцип эффекта Холла предполагает, что магнитная сила в токе приводит к скученности на конце трубы или провода.

Электромагнитный принцип теперь объясняет явления, лежащие в основе эффекта Холла, гораздо лучше. Теория этого ученого, безусловно, намного опередила свое время.

Лишь два десятилетия спустя, с введением полупроводников, работы по исследованию эффекта Холла были эффективно использованы.

Первоначально этот принцип использовался для классификации химических образцов.

Позднее датчики Холла (с использованием полупроводниковых соединений арсенида индия) стали источником для измерения постоянного или статического магнитного поля без поддержания датчика в движении.

Через десятилетие, в 1960-х годах, появились кремниевые полупроводники. Это было время, когда элементы Холла были объединены со встроенными усилителями, и таким образом выключатель Холла был представлен миру.

Принцип работы эффекта Холла

Эффект получения измеримого напряжения, как сказано выше, называется эффектом Холла.

Теория за принципом эффекта Холла

Напряжение Холла прямо пропорционально электрическому току, и прямо пропорционально приложенному магнитному полю.

Формула эффекта Холла

Вот некоторые математические выражения, которые широко используются в вычислениях эффекта Холла:

Напряжение Холла

Напряжение Холла представлено V H. Формула для напряжения Холла:

Где:
I — Ток, протекающий через датчик
B — напряженность магнитного поля
q — заряд
n — количество носителей заряда на единицу объема
d — толщина датчика

Коэффициент Холла

Он представлен RH. Формула для коэффициента Холла: RH равно 1 / (qn). Коэффициент Холла (R H) положителен, если число отверстий положительного заряда больше, чем число электронов отрицательного заряда. Аналогично, коэффициент Холла (RH) отрицателен, если число отрицательных зарядовых электронов больше, чем число отверстий положительного заряда.

Концентрация несущей заряда

Холловская мобильности

Холловская мобильность для электронов представлена как «μ n», а для отверстий — как «μ p». Математическое выражение для мобильности Холла:

Где:
μ n — проводимость за счет электронов
μ p — проводимость благодаря отверстиям

Плотность магнитного потока

Плотность магнитного потока обозначена буквой «B». Формула для плотности магнитного потока:

Применение принципа эффекта Холла

Принцип эффекта Холла используется в следующих случаях:

Оборудование для измерения магнитного поля.
Множитель приложений для обеспечения фактического умножения.
Тестер эффекта Холла для измерения постоянного тока.
Измерение фазового угла. Например, при измерении углового положения коленчатого вала, чтобы точно выровнять угол зажигания свечей зажигания
Датчики линейных или угловых перемещений. Например, чтобы определить положение автомобильных сидений и ремней безопасности и выступить в роли блокировки для управления подушкой безопасности.
Датчики приближения.
Датчики с эффектом Холла
Для определения скорости вращения колеса и, соответственно, помощи антиблокировочной тормозной системы (ABS).

Как эффект Холла можно использовать для определения типа используемого полупроводника

Коэффициент Холла говорит обо всем. Если коэффициент Холла отрицателен, это означает, что основными носителями заряда являются электроны.

И поскольку число электронов больше по сравнению с отверстиями в полупроводниках n-типа, это ясно указывает на то, что испытываемый полупроводник n-типа. Аналогичным образом, если коэффициент Холла положительный, это означает, что основными носителями заряда являются дырки.

И поскольку число отверстий больше по сравнению с электронами в полупроводниках p-типа, это ясно указывает на то, что испытываемый полупроводник p-типа.

Источник: https://meanders.ru/jeffekta-holla-princip-raboty-objasnenie-teorii-formula.shtml

11.7: Эффект Холла — Physics LibreTexts

Цели обучения

К концу этого раздела вы сможете:

Объясните сценарий, в котором магнитное и электрическое поля пересекаются, и их силы уравновешивают друг друга, когда заряженная частица движется через селектор скорости.
Сравните, как движутся носители заряда в проводящем материале, и объясните, как это связано с эффектом Холла

В 1879 г. Холл разработал эксперимент, который можно использовать для определения знака преобладающих носителей заряда в проводящем материале.С исторической точки зрения, этот эксперимент был первым, кто продемонстрировал, что носители заряда в большинстве металлов отрицательны.

Посетите этот веб-сайт, чтобы найти дополнительную информацию об эффекте Холла.

Мы исследуем эффект Холла , изучая движение свободных электронов вдоль металлической полосы шириной l в постоянном магнитном поле (рисунок \ (\ PageIndex {1} \)). Электроны движутся слева направо, поэтому магнитная сила, которую они испытывают, толкает их к нижнему краю полосы.Это оставляет избыток положительного заряда на верхнем крае полосы, в результате чего электрическое поле E направлено сверху вниз. Концентрация заряда на обоих краях увеличивается до тех пор, пока электрическая сила, действующая на электроны в одном направлении, не уравновешивается магнитной силой, действующей на них в противоположном направлении. Равновесие достигается когда:

\ [eE = ev_d B \ label {11.24} \]

, где e — величина заряда электрона, \ (v_d \) — скорость дрейфа электронов, а E — величина электрического поля, создаваемого разделенным зарядом.Решение этой проблемы для скорости дрейфа дает

\ [v_d = \ frac {E} {B}. \ label {11.25} \]

Рис. \ (\ PageIndex {1} \): В эффекте Холла возникает разность потенциалов между верхним и нижним краями металлической полосы, когда движущиеся носители заряда отклоняются магнитным полем. а) эффект Холла для отрицательных носителей заряда; (б) Эффект Холла для положительных носителей заряда.
Сценарий, в котором электрическое и магнитное поля перпендикулярны друг другу, называется ситуацией скрещенного поля.Если эти поля создают равные и противоположные силы на заряженную частицу со скоростью, равной силам, эти частицы могут проходить через устройство, называемое селектором скорости , без отклонения. Эта скорость представлена в уравнении \ ref {11.26}. Любая другая скорость заряженной частицы, посланной в те же поля, будет отклоняться магнитной силой или электрической силой.
Возвращаясь к эффекту Холла, если ток в полосе равен I , то по току и сопротивлению мы знаем, что
\ [I = nev_dA \ label {11.26} \]
, где n — количество носителей заряда в объеме, а A — площадь поперечного сечения полоски. Комбинируя уравнения для \ (v_d \) и I , получаем
\ [I = ne \ left (\ frac {E} {B} \ right) A. \ label {11.27} \]
Поле E связано с разностью потенциалов V между краями полосы на
\ [E = \ frac {V} {l}. \ label {11.28} \]
Величина \ (V \) называется потенциалом Холла и может быть измерена с помощью вольтметра.Наконец, объединение уравнений для I и E дает нам
\ [V = \ dfrac {IBl} {neA} \ label {hallV} \]
, где верхний край полосы на рисунке \ (\ PageIndex {1} \) положителен по отношению к нижнему краю.
Мы также можем объединить уравнение \ ref {11.24} и уравнение \ ref {11.28}, чтобы получить выражение для напряжения Холла через магнитное поле:
\ [V = Blv_d. \]
Что делать, если носители заряда положительны, как на рисунке \ (\ PageIndex {1} \)? Для того же тока I величина V все еще определяется уравнением \ ref {hallV}.Однако теперь верхний край отрицателен по отношению к нижнему краю. Следовательно, просто измерив знак В , мы можем определить знак основных носителей заряда в металле.
Измерения потенциала Холла показывают, что электроны являются основными носителями заряда в большинстве металлов. Однако потенциалы Холла показывают, что для некоторых металлов, таких как вольфрам, бериллий и многих полупроводников, большинство носителей заряда являются положительными. Оказывается, проводимость за счет положительного заряда вызвана миграцией отсутствующих электронных узлов (так называемых дырок) на ионах.Дырочная проводимость изучается позже в Физике конденсированного состояния.
Эффект Холла можно использовать для измерения магнитных полей. Если материал с известной плотностью носителей заряда n поместить в магнитное поле и измерить V , то поле можно определить с помощью уравнения \ ref {11.29}. В исследовательских лабораториях, где поля электромагнитов, используемых для точных измерений, должны быть чрезвычайно стабильными, «зонд Холла» обычно используется как часть электронной схемы, регулирующей поле.3 \, N / C \) соответственно. (а) Какой должна быть скорость электронного пучка, чтобы пересечь скрещенные поля без отклонения? Если электрическое поле выключено, (б) каково ускорение электронного пучка и (в) каков радиус кругового движения, которое возникает в результате?
Стратегия
Электронный луч не отклоняется ни магнитным, ни электрическим полями, если эти силы уравновешены. На основе этих уравновешенных сил мы вычисляем скорость луча.{-3} м. \]
Значение
Если бы электроны в пучке имели скорости выше или ниже ответа в части (а), эти электроны имели бы более сильную результирующую силу, создаваемую либо магнитным, либо электрическим полем. Следовательно, только электроны с этой конкретной скоростью смогут пройти.
Холловский потенциал в серебряной ленте
На рисунке \ (\ PageIndex {2} \) показана серебряная лента, поперечное сечение которой составляет 1,0 см на 0,20 см. По ленте слева направо течет ток 100 А, и она находится в однородном магнитном поле величиной 1.{28} \) электронов на кубический метр для серебра, найти потенциал Холла между краями ленты.
Рисунок \ (\ PageIndex {2} \): Показано определение потенциала Холла в серебряной ленте в магнитном поле.
Стратегия
Поскольку большинство носителей заряда — электроны, полярность напряжения Холла такая, как показано на рисунке. Значение напряжения Холла рассчитывается с помощью уравнения \ ref {hallV}.
Решение
При вычислении напряжения Холла нам необходимо знать ток через материал, магнитное поле, длину, количество носителей заряда и площадь.{28} \) электронов на кубический метр, ширина 2,0 см и толщина 0,10 см. Что такое магнитное поле, если I = 50 А и потенциал Холла
\ (4.0 \, \ mu V \) и
\ (6,0 \, \ мю В \)?
Ответьте на
1,1 т
Ответ б
1,6 т
Авторы и авторство
Сэмюэл Дж.Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эффект Холла | Физика
Цели обучения
К концу этого раздела вы сможете:
Опишите эффект Холла.
Вычислите ЭДС Холла в проводнике с током.
Мы видели влияние магнитного поля на свободно движущиеся заряды. Магнитное поле также влияет на заряды, движущиеся в проводнике. Одним из результатов является эффект Холла, который имеет важные последствия и приложения. На рисунке 1 показано, что происходит с зарядами, движущимися через проводник в магнитном поле. Поле перпендикулярно дрейфовой скорости электронов и ширине проводника. Обратите внимание, что условный ток находится справа в обеих частях рисунка. В части (а) электроны переносят ток и движутся влево.В части (b) положительные заряды переносят ток и движутся вправо. Движущиеся электроны ощущают магнитную силу по направлению к одной стороне проводника, оставляя чистый положительный заряд на другой стороне. Это разделение зарядов создает напряжение ε , известное как эдс Холла , на проводнике. Создание напряжения на проводнике с током с помощью магнитного поля известно как эффект Холла в честь Эдвина Холла, американского физика, который открыл его в 1879 году.
Рис. 1. Эффект Холла. (а) Электроны движутся в этом плоском проводнике влево (обычный ток вправо). Магнитное поле находится прямо за пределами страницы, оно представлено точками в кружках; он воздействует на движущиеся заряды, создавая напряжение ε , ЭДС Холла, поперек проводника. (b) Положительные заряды, движущиеся вправо (обычный ток также вправо), смещаются в сторону, создавая ЭДС Холла противоположного знака, –ε . Таким образом, если направление поля и тока известны, знак носителей заряда можно определить по эффекту Холла.
Одним из очень важных способов использования эффекта Холла является определение того, переносят ли ток положительный или отрицательный заряд. Обратите внимание, что на Рисунке 1 (b), где положительные заряды переносят ток, ЭДС Холла имеет знак, противоположный тому, когда отрицательные заряды переносят ток. Исторически эффект Холла использовался, чтобы показать, что электроны переносят ток в металлах, а также показывает, что положительные заряды переносят ток в некоторых полупроводниках. Эффект Холла сегодня используется в качестве исследовательского инструмента для исследования движения зарядов, их скорости и плотности дрейфа и т. Д. В материалах.В 1980 году было обнаружено квантование эффекта Холла — примера квантового поведения макроскопического объекта.
Эффект Холла имеет и другие применения: от определения скорости кровотока до точного измерения напряженности магнитного поля. Чтобы исследовать их количественно, нам нужно выражение для ЭДС Холла, ε , поперек проводника. Рассмотрим баланс сил на движущемся заряде в ситуации, когда B , v и l взаимно перпендикулярны, как показано на рисунке 2.Хотя магнитная сила перемещает отрицательные заряды в одну сторону, они не могут накапливаться без ограничений. Электрическое поле, вызванное их разделением, противодействует магнитной силе, F = qvB , и электрическая сила, F _e = qE , в конечном итоге возрастает, чтобы сравняться с ней. То есть
qE = qvB
или
E = vB.
Обратите внимание, что электрическое поле E однородно по проводнику, потому что магнитное поле B однородно, как и провод.Для однородного электрического поля соотношение между электрическим полем и напряжением составляет E = ε / l , где l — ширина проводника, а ε — эдс Холла. Ввод этого в последнее выражение дает
[латекс] \ frac {\ epsilon} {l} = vB [/ латекс].
Решение этого для ЭДС Холла дает
ε = Blv (B, v и l, взаимно перпендикулярно),
, где ε — напряжение эффекта Холла на проводнике шириной l , по которому заряды движутся со скоростью v .
Рис. 2. ЭДС Холла ε создает электрическую силу, которая уравновешивает магнитную силу движущихся зарядов. Магнитная сила вызывает разделение зарядов, которое накапливается до тех пор, пока не будет уравновешено электрической силой, равновесие, которое достигается быстро.
Одно из наиболее распространенных применений эффекта Холла — измерение напряженности магнитного поля B . Такие устройства, называемые датчиками Холла , могут быть очень маленькими, что позволяет точно отображать положение.Датчики Холла также можно сделать очень точными, обычно это достигается тщательной калибровкой. Еще одно применение эффекта Холла — измерение потока жидкости в любой жидкости, имеющей свободные заряды (в большинстве случаев). (См. Рис. 3.) Магнитное поле, приложенное перпендикулярно направлению потока, создает ЭДС Холла ε , как показано. Отметим, что знак ε зависит не от знака зарядов, а только от направлений B и v . Величина ЭДС Холла равна, где l — диаметр трубы, так что средняя скорость v может быть определена из ε при условии, что известны другие факторы.
Рис. 3. Эффект Холла можно использовать для измерения потока жидкости в любой жидкости, имеющей свободные заряды, например в крови. ЭДС Холла ε измеряется поперек трубки, перпендикулярной приложенному магнитному полю, и пропорциональна средней скорости v .
Пример 1. Расчет ЭДС Холла: эффект Холла для кровотока
Датчик потока на эффекте Холла помещают на артерию, прикладывая к ней магнитное поле напряжением 0,100 Тл, в установке, аналогичной показанной на рисунке 3.Что такое ЭДС Холла при внутреннем диаметре сосуда 4,00 мм и средней скорости кровотока 20,0 см / с?
Стратегия
Поскольку B , v и l взаимно перпендикулярны, уравнение ε = Blv может использоваться для нахождения ε .
Решение
Ввод данных значений для B , v и l дает
[латекс] \ begin {array} {lll} \ epsilon & = & Blv = \ left (0.{-3} \ text {m} \ right) \ left (0.200 \ text {m / s} \ right) \\ & = & 80.0 \ text {} \ mu \ text {V} \ end {array} \\ [/ латекс]
Обсуждение
Это среднее выходное напряжение. Мгновенное напряжение зависит от пульсации кровотока. В этом типе измерения напряжение невелико. ε особенно трудно измерить, потому что есть напряжения, связанные с работой сердца (напряжения ЭКГ), которые имеют порядок милливольт. На практике эту трудность преодолевают путем приложения переменного магнитного поля, так что ЭДС Холла является переменным током той же частоты.Усилитель может очень избирательно выбирать только подходящую частоту, устраняя сигналы и шум на других частотах.
Сводка раздела
Эффект Холла — это создание магнитным полем напряжения ε , известного как ЭДС Холла, на проводнике с током.
ЭДС Холла определяется выражением
ε = Blv (B, v и l, взаимно перпендикулярно)
для проводника шириной l , по которому заряды движутся со скоростью v .
Концептуальные вопросы
1. Обсудите, как можно использовать эффект Холла для получения информации о плотности свободных зарядов в проводнике. (Подсказка: подумайте, как связаны скорость дрейфа и течение.)
Задачи и упражнения
1. Большой водовод имеет диаметр 2,50 м, а средняя скорость воды составляет 6,00 м / с. Найдите напряжение Холла, возникающее, если труба проложена перпендикулярно полю Земли 5,00 × 10 ⁻⁵ -T.
2.Какое напряжение Холла создается полем 0,200 Тл, приложенным к аорте диаметром 2,60 см при скорости кровотока 60,0 см / с?
3. (a) Какова скорость сверхзвукового летательного аппарата с размахом крыла 17,0 м, если он испытывает напряжение Холла 1,60 В между законцовками крыла при горизонтальном полете над северным магнитным полюсом, где напряженность поля Земли равна 8,00 × 10 ^— ⁵ T? (б) Объясните, почему из-за этого напряжения Холла протекает очень мало тока.
4.Немеханический счетчик воды может использовать эффект Холла, прикладывая магнитное поле к металлической трубе и измеряя создаваемое напряжение Холла. Какова средняя скорость жидкости в трубе диаметром 3,00 см, если поле 0,500 Тл на ней создает напряжение Холла 60,0 мВ?
5. Рассчитайте напряжение Холла, наведенное на сердце пациента во время сканирования с помощью аппарата МРТ. Приблизьте проводящий путь на стенке сердца проволокой длиной 7,50 см, которая движется со скоростью 10,0 см / с перпендикулярно к 1.Магнитное поле 50 Тл.
6. Зонд Холла, откалиброванный для показаний 1,00 мкВ при помещении в поле 2,00 Тл, помещают в поле 0,150 Тл. Какое у него выходное напряжение?
8. Покажите, что напряжение Холла на проводах, сделанных из одного и того же материала, несущих одинаковые токи и находящихся в одном и том же магнитном поле, обратно пропорционально их диаметрам. (Подсказка: подумайте, как скорость дрейфа зависит от диаметра проволоки.)
9. Пациента с кардиостимулятором по ошибке сканируют на МРТ.Отрезок провода кардиостимулятора длиной 10,0 см движется со скоростью 10,0 см / с перпендикулярно магнитному полю аппарата МРТ, при этом индуцируется напряжение Холла 20,0 мВ. Какая напряженность магнитного поля?
Глоссарий
Эффект Холла:
Создание напряжения на проводнике с током с помощью магнитного поля
ЭДС Холла:
электродвижущая сила, создаваемая проводником с током магнитным полем, ε = Blv
Избранные решения проблем и упражнения
1.7,50 × 10 ⁻⁴ В
3. (a) 1,18 × 10 ³ м / с (b) После установления ЭДС Холла толкает заряды в одном направлении, а магнитная сила действует в противоположном направлении, что не приводит к действию результирующей силы на заряды. Следовательно, в направлении ЭДС Холла ток не течет. Это то же самое, что и в проводнике с током — ток не течет в направлении ЭДС Холла.
5. 11,3 мВ
7. 1,16 мкВ
9. 2.00 т
2.1.3 Эффект Холла
© Х. Фёлль (сценарий MaWi 2)
Посчитать относительно легко величина напряжения Холла U _Холл , индуцированный магнитным полем B .
Прежде всего отметим, что мы также должны иметь электрическое поле E параллельно j потому что это движущая сила тока.
Во-вторых, мы знаем, что магнитное поле под прямым углом к току вызывает силу на движущемся носители, т.н. Lorentz force ф. _л. , что дает
Мы должны взять скорость дрейфа v _D носителей, потому что другой скорости (и силы, вызванные этими компонентами) сокращаются до нуля на средний.Векторное произведение гарантирует, что F _L равно перпендикулярно v _D и B .
Обратите внимание, что вместо обычное слово «электрон» используется нейтральный термин носитель , потому что в принципе электрический ток также может переноситься заряженными частицами, отличными от электронов, например положительно заряженные ионы.Помните простое, но важная картина дана раньше!
Для указанной выше геометрии сила Лоренца F _L имеет только компонент в y — направление, и мы можем использовать для него скалярное уравнение. F _y предоставляется
F _y = — q · v _{D, x} · B _z
Мы должны быть немного осторожно: мы знаем, что сила действует в направлении y , но мы не больше знаю знак.Он изменяется, если либо q , v _D или B _z меняет направление, и мы должны знать об этом.
Однако важно отметить, что для фиксированной плотности тока j _x направление силы Лоренца не зависит от знака заряда носителей — знак заряда и знак скорости дрейфа точно отменяют друг друга.
с v _D = µ · E и µ = мобильность носителей, получаем довольно простое уравнение для силы
F _y = — | q | · Μ · E _x · B _z
Это означает, что ток несущие будут отклоняться от прямой в направлении y .Другими словами, есть составляющая скорости в y — направление и поверхности перпендикулярны y -направление будет заряжаться, как только текущий (или магнитное поле) включается. Обводы носителей будут иметь вид это:
Зарядка поверхностей неизбежно, потому что некоторые носители в конечном итоге окажутся на поверхности где они «застряли».
Обратите внимание, что знак заряда для данной поверхности зависит от знака заряда носителей. Отрицательно заряженные электроны ( e ^— на картинке) оказываются на поверхность, противоположная положительно заряженным носителям (называется h ⁺ на картинке).
Обратите внимание, что направление сила F _y одинакова для обоих типов перевозчиками, просто потому что и q и v _D изменить знаки в формуле силы
Затем поверхностный заряд вызывает электрическое поле E _y in y — направление, которое противостоит силе Лоренца; он пытается вернуть носителей обратно.
В равновесие , сила Лоренца F _y и сила электрического поля E _y in y -направление (которое, конечно, просто q · E _y ) должно быть равно противоположному приметы. Таким образом, получаем
— q · E _y = — | q | · Μ · E _x · B _z
E _y = знак ( q ) · µ · E _x · B _z
Напряжение Холла U _Холл теперь просто поле в y -направление, умноженное на размерность d _y дюйм y — направление.
Понятно, что (легко измеряемое) напряжение Холла составляет прямого измерить подвижности µ задействованных носителей, и что его знак или полярность изменится если знак движения зарядов изменится.
Принято определить коэффициент Холла R _Холл для данного материала.
Это можно сделать в разными, но равнозначными способами. в ссылку мы смотрим на определение, которое особенно подходит для измерений. Здесь мы используем следующее определение:
Другими словами, мы ожидаем, что напряжение Холла E _y · d _y (с d _y = размер в y -направление) пропорционально току (плотности) j и напряженность магнитного поля B , которые ведь основные экспериментальные параметры (помимо тривиальных размеров экз):
E _y = R _Холл · B _z · j _x
Коэффициент Холла равен параметр материала, потому что мы получим разные числа для R _Холл , если мы проводим эксперименты с идентичным магнитным поля и плотности тока, но из разных материалов.Коэффициент Холла, как упомянутый ранее, имеет интересные свойства:
R _Зал изменит свой знак, если знак носителей изменяется, потому что тогда E _y меняет свое подписать тоже. Таким образом, он самым недвусмысленным образом указывает на положительный или отрицательные заряды несут ток.
R _Холл позволяет получить мобильность µ носителей тоже, как мы сразу увидим.
R _Hall легко вычисляется: Используя уравнение для E _y сверху, и основное уравнение j _x = s · E _x , получаем для отрицательно носителей заряда:
R _Холл = — µ · E _x · B _z
s · E _x · B _z = — µ
с = — µ
| q | · n · µ = — 1
| q | · n
Синяя часть соответствует вывод, приведенный в ссылке; n (очевидно) концентрация носителя.
Если известен коэффициент Холла или концентрация носителей, то Эффект Холла можно использовать для измерения напряженности магнитного поля B ( не так-то просто иначе!).
Измерения коэффициента Холла материалов с известной проводимостью (что-то легко измеримое), таким образом, мы получаем напрямую подвижность носителей, ответственных для проводимости.
Знак минус выше получается для электронов , то есть отрицательных зарядов.
Если бы положительно заряженные носители постоянная Холла будет положительна .
Обратите внимание, что пока это не всегда просто для измерения числового значения напряжения Холла и, следовательно, R с хорошей точностью, это самая простая вещь в мире для измерения полярность напряжения.
Давайте посмотрим на несколько экспериментальные данные:
Материал Ли Cu Ag Au Al Be В Полупроводники
(е.грамм. Si , G e , GaAs , InP , …)
R
(× 10 ^–24)
cgs ед. –1,89 –0,6 –1,0 –0,8 +1 136 +2,7 +1,774 положительных или отрицательных значения, в зависимости от «допинг»
Комментарии:
1. положительных значений для металлы измерялись в несколько особых условиях (низкие температуры; монокристаллы с особой ориентацией), для других условий отрицательные значения также могут быть получены.
2. Единицы не важны в деле, а умножение на 9 · 10 ¹³ дает значение в м ³ / Кулон
Эффект Холла
Эффект Холла позволяет различать положительные заряды, текущие в одном направлении, и отрицательные заряды, текущие в другом.Это также обычный способ измерения силы магнитного поля.
Для начала изобразите провод квадратного сечения, по которому ток идет вправо. На страницу направлено однородное магнитное поле.
Если ток состоит из положительных зарядов, текущих вправо, в каком направлении действует магнитная сила на заряды?
Вверх
Вниз
слева
Правый
На страницу
Вне страницы
Усилие увеличено.Положительные заряды отклоняются вверх, оставляя дефицит положительного заряда (то есть чистый отрицательный заряд) внизу. Это похоже на набор заряженных параллельных пластин с направленным вниз электрическим полем. Электрическое поле нарастает до тех пор, пока сила, испытываемая зарядами в этом электрическом поле, не станет равной силе, приложенной к зарядам магнитным полем, и противоположной ей.
Электрическое поле связано с разностью потенциалов на проводе, которую можно измерить с помощью вольтметра.Это известно как напряжение Холла V _H. Если предположить, что электрическое поле однородно, напряжение Холла будет:
V _H = -Ed, где d — ширина провода.
Сила, действующая на заряды из-за электрического поля, уравновешивается магнитной силой, поэтому:
qE = qv _d B и E = v _d B, поэтому напряжение Холла составляет:
V _H = -v _d Bd, где v _d — скорость дрейфа зарядов.
Напряжение Холла пропорционально магнитному полю, поэтому измерение напряжения можно легко превратить в измерение B. Или, в известном магнитном поле, напряжение Холла можно использовать для измерения скорости дрейфа.
А что, если заряды, протекающие по проводу, действительно отрицательные, текут налево? В каком направлении действует магнитная сила на заряды?
Вверх
Вниз
слева
Правый
На страницу
Вне страницы
Магнитное поле снова отклоняет заряды к верху провода.Это создает электрическое поле, противоположное по направлению полю, полученному с помощью положительных зарядов, меняя знак напряжения Холла. Итак, выяснить, состоит ли ток из положительных или отрицательных зарядов, так же просто, как проверить знак напряжения Холла.
Эффект Холла
Эффект Холла
Далее: Окружной закон Ампера Up: Магнетизм Предыдущая: Заряженная частица в Мы неоднократно заявляли, что мобильные платежи в общепринятый проводящие материалы заряжены отрицательно (по сути, это электроны).Есть ли какие-либо прямые экспериментальные доказательства того, что это правда? Собственно, есть. Мы можем используйте явление, называемое эффектом Холла , чтобы определить, подвижные заряды в данном проводнике заряжены положительно или отрицательно. Исследуем этот эффект.
Рассмотрим тонкую плоскую однородную ленту из проводящего материала, которая ориентирован так, чтобы его плоская сторона была перпендикулярна однородной магнитное поле — см. рис. 26. Предположим, что мы пропускаем ток по длине ленты.Есть две альтернативы. Либо текущий несет положительный заряд двигаясь слева направо (на рисунке), или его переносят отрицательные заряды, движущиеся в противоположном направлении.
Предположим, что ток переносится положительными зарядами, движущимися слева направо. Эти обвинения отклоняются вверх (на рисунке) магнитным полем. Таким образом, верхний край ленты становится заряжен положительно, а нижний край — отрицательно.Следовательно, существует положительная разность потенциалов между верхними и нижние края ленты. Эта разность потенциалов называется напряжением Холла .
Предположим теперь, что ток переносится отрицательными зарядами. двигаясь справа налево. Эти заряды также отклоняются на вверх на магнитным полем. Таким образом, верхний край ленты становится отрицательно заряженной, а нижний край становится положительно заряженный. Отсюда следует, что напряжение Холла ( i.е. г. разность потенциалов между верхним и нижним краями ленты) в данном случае отрицательное значение .
Рисунок 26: Эффект Холла для положительных носителей заряда (слева) и отрицательных носители заряда (справа).

Понятно, что можно определить знак мобильных зарядов в токопроводящий проводник путем измерения напряжения Холла. Если напряжение положительный, то заряды мобильных устройств положительны (при условии, что магнитное поле и ток ориентированы, как показано на рисунок), тогда как если напряжение отрицательный, то мобильные заряды отрицательны.Если бы мы должны были выполнить В этом эксперименте мы обнаружим, что подвижные заряды в металлах всегда отрицательны (потому что они электроны). Однако в некоторых типах полупроводников подвижные заряды оказались положительными. Эти носители положительного заряда называются дырками, . Дырки фактически лишены электронов в атомной решетке полупроводник, но они действуют как положительные заряды.
Давайте исследуем величину напряжения Холла.Предположим, что мобильный каждый из зарядов обладает зарядом и движется по ленте вместе с скорость дрейфа . Магнитная сила, действующая на данный мобильный заряд имеет величину, поскольку заряд движется существенно перпендикулярно магнитному полю. В установившемся состоянии эта сила уравновешивается электрической силой из-за накопления зарядов по верхнему и нижнему краю ленты. Если напряжение Холла , а ширина ленты равна, то электрическая поле, указывающее от верхнего к нижнему краю ленты, величины.Теперь электрическая сила на мобильном заряде является . Эта сила действует против магнитной силы. В устойчивом состоянии
(169)

давая
(170)

Обратите внимание, что напряжение Холла прямо пропорционально величине магнитное поле. Фактически это свойство Напряжение Холла используется в приборах, называемых датчиками Холла , которые используются для измерения напряженности магнитного поля.
Предположим, что толщина проводящей ленты равна, и что она содержит мобильные носители заряда на единицу объема. Отсюда следует, что полный ток протекающий через ленту можно написать
(171)

поскольку все мобильные заряды содержатся в прямоугольном объеме длиной, шириной , и толщину, обтекают заданную точку на ленте за одну секунду. Комбинируя уравнения. (170) и (171), получаем
(172)

Понятно, что напряжение Холла пропорционально току, протекающему через лента, и напряженность магнитного поля, и обратно пропорциональна плотности подвижных зарядов в ленте и толщине ленту.Таким образом, для создания чувствительного зонда Холла (, т. Е. , который дает большое напряжение Холла в наличие небольшого магнитного поля), нам нужно взять тонкую ленту некоторый материал, который имеет относительно мало мобильных зарядов на единицу объем (, например, , полупроводник), а затем пропустите через него большой ток.

Далее: Окружной закон Ампера Up: Магнетизм Предыдущая: Заряженная частица в
Ричард Фицпатрик 2007-07-14
Измерения эффекта Холла
Электрические характеристики материалов развивались на трех уровнях понимания.В начале 1800-х годов сопротивление R и проводимость G считались измеримыми физическими величинами, которые можно было получить с помощью двухконтактных измерений I-V (т. Е. Тока I , напряжения В ). Позже стало очевидно, что одно только сопротивление не является достаточно полным, поскольку разные формы образцов дают разные значения сопротивления. Это привело к пониманию (второй уровень) того, что требуется внутреннее свойство материала, такое как удельное сопротивление (или проводимость), на которое не влияет конкретная геометрия образца.Впервые это позволило ученым количественно оценить токонесущую способность материала и провести значимые сравнения между различными образцами. Теории электропроводности строились с разной степенью успеха, но до появления квантовой механики не было разработано общеприемлемого решения проблемы электрического переноса. Это привело к определениям плотности носителей n и мобильности µ (третий уровень понимания), которые сегодня способны выполнять даже самые сложные электрические измерения.
Эффект Холла и сила Лоренца
Основным физическим принципом, лежащим в основе эффекта Холла, является сила Лоренца. Когда электрон движется в направлении, перпендикулярном приложенному магнитному полю, он испытывает силу, действующую перпендикулярно обоим направлениям, и движется в ответ на эту силу и силу внутреннего электрического поля. Сила Лоренца дается

Эффект Холла проиллюстрирован на рисунке 1 для образца в форме стержня, в котором заряд переносится электронами.Постоянный ток I протекает через стержень, и весь стержень подвергается воздействию однородного магнитного поля B , которое направлено в экран перпендикулярно току. Поскольку электроны движутся через магнитное поле, они подвергаются действию восходящей силы Лоренца и, таким образом, дрейфуют к вершине стержня, сохраняя при этом свое горизонтальное движение. Это приводит к накоплению отрицательного заряда с одной стороны стержня и положительного заряда с другой из-за отсутствия электронов.Это приводит к разности потенциалов между двумя сторонами образца, которую можно измерить как напряжение Холла V _H. (Обратите внимание, что сила, действующая на отверстия, направлена с одной стороны из-за их противоположной скорости и положительного заряда.)
Рисунок 1: Иллюстрация эффекта Холла в стержне из проводящего материала.
Это поперечное напряжение представляет собой напряжение Холла В _H, а его величина равна IB / qnd , где I — ток, B — магнитное поле, d — толщина образца, и q (1.602 x 10 ^-19 C) — элементарный заряд. В некоторых случаях удобно использовать плотность слоя или листа ( n _s = nd ) вместо насыпной плотности. Тогда получается уравнение
(1)
Таким образом, измеряя напряжение Холла В _H и по известным значениям I , B и q , можно определить плотность слоев n _s носителей заряда в полупроводниках. .Если измерительное устройство настроено, как показано, напряжение Холла будет отрицательным для полупроводников типа n и положительным для полупроводников типа p . Листовое сопротивление R _S полупроводника может быть удобно определено с помощью метода измерения удельного сопротивления Ван-дер-Пау. Поскольку сопротивление листа включает в себя как плотность, так и подвижность листа, подвижность Холла можно определить из уравнения

(2)
Если известна толщина проводящего слоя d , можно определить объемное удельное сопротивление ( r = R _S d ) и объемную плотность ( n = n _S/ d ).
Техника Ван дер Пау
Чтобы определить как подвижность µ , так и плотность листа n _s, необходима комбинация измерения удельного сопротивления и измерения Холла. Мы обсуждаем здесь метод Ван дер Пау, который из-за его удобства широко используется в полупроводниковой промышленности для определения удельного сопротивления однородных образцов (ссылки 3 и 4). Первоначально изобретенный Ван дер Пау, используется произвольно сформированный (но просто связанный, т.е.е. без отверстий или непроводящих островков или включений) образец тонкой пластины, содержащий четыре очень маленьких омических контакта, размещенных на периферии (предпочтительно в углах) пластины. Примеры конфигураций Ван дер Пау показаны на рисунке 2.
Рисунок 2. Примеры возможных конфигураций Ван дер Пау и их предпочтения [12]
Цель измерения удельного сопротивления — определить сопротивление листа R _S.Ван дер Пау продемонстрировал, что на самом деле существует два характеристических сопротивления: R _A и R _B, связанных с соответствующими клеммами, показанными на рис. 2. R _A и R _B связаны с сопротивлением листа R _S через уравнение Ван дер Пау
(3)
, который можно решить численно для R _S.
Объемное электрическое сопротивление r можно рассчитать с помощью
(4)
Чтобы получить два характеристических сопротивления, один прикладывает постоянный ток I к контакту 1 и вне контакта 2 и измеряет напряжение В ₄₃ между контактом 4 и контактом 3.Затем прикладывают ток I к контакту 2 и вне контакта 3 при измерении напряжения В ₁₄ от контакта 1 к контакту 4, используя геометрию, показанную на рисунке 3. R _A и R _B вычисляются с помощью следующих выражений:
и
(5)

Цель измерения Холла в технике Ван-дер-Пау — определить плотность носителей листа n _s путем измерения напряжения Холла В _H.Измерение напряжения Холла состоит из серии измерений напряжения с постоянным током I и постоянным магнитным полем B , приложенным перпендикулярно плоскости образца. Удобно, чтобы тот же образец, снова показанный на рис. 3, также можно было использовать для измерения Холла. Чтобы измерить напряжение Холла В _H, ток I пропускается через противоположную пару контактов 1 и 3, а напряжение Холла В _H (= В ₂₄) измеряется через оставшаяся пара контактов 2 и 4.После получения напряжения Холла В _H плотность несущей листа n _s может быть вычислена с помощью n _s = IB / q | V _H | из известных значений I , B и q .
Есть практические аспекты, которые необходимо учитывать при проведении измерений Холла и удельного сопротивления. Основными проблемами являются (1) качество и размер омического контакта, (2) однородность образца и точное определение толщины, (3) термомагнитные эффекты из-за неоднородной температуры и (4) фотопроводящие и фотоэлектрические эффекты, которые можно минимизировать путем измерения в темноте. .Кроме того, поперечные размеры образца должны быть большими по сравнению с размером контактов и толщиной образца. Наконец, необходимо точно измерить температуру образца, напряженность магнитного поля, электрический ток и напряжение.
Дополнительная информация о температурной зависимости измерений Холла и о том, как эту зависимость можно использовать, обсуждается на странице температурной зависимости
.
Тип имеющихся носителей, т.е. тип n или p, очень важен. Более подробно эта область обсуждается на странице типа перевозчика
.
Список литературы
http: // www.eeel.nist.gov/812/effe.htm
«Стандартные методы испытаний для измерения удельного сопротивления и коэффициента Холла и определения подвижности Холла в монокристаллических полупроводниках», обозначение ASTM F76, Ежегодная книга стандартов ASTM, Vol. 10.05 (2000).
Холл Э. Х. О новом действии магнита на электрический ток, Amer. J. Math. 2 , 287-292 (1879).
L. J. van der Pauw, «Метод измерения удельного сопротивления и эффекта Холла дисков произвольной формы», Philips Res.Repts. 13 , 1-9 (1958).
Л. Дж. Ван дер Пау, «Метод измерения удельного сопротивления и коэффициента Холла на ламелях произвольной формы», Philips Tech. Ред. 20 , 220-224 (1958).
Э. Х. Путли, Эффект Холла и связанные с ним явления, Баттервортс, Лондон (1960).
D. C. Look, Электрические характеристики материалов и устройств на основе GaAs, John Wiley & Sons, Чичестер (1989).
Д. К. Шредер, Характеристики полупроводниковых материалов и устройств, 2-е издание, John Wiley & Sons, Нью-Йорк (1998).
Р. Чван, Б. Дж. Смит и К. Р. Кроуэлл, «Влияние размера контакта на метод Ван дер Пау для измерения удельного сопротивления и коэффициента Холла», Solid-State Electronics 17 , 1217-1227 (1974).
Д. Л. Роде, К. М. Вулф и Г. Э. Стилман, «Зависимость фактора Холла от магнитного поля для изотропных сред», J. Appl. Phys. 54 , 10-13 (1983).
Д. Л. Роде, «Перенос электронов в низком поле», Полупроводники и полуметаллы 10 , 1-89 (1975).
http://en.wikipedia.org/wiki/File:VanderPauwContactPlacement.jpg
Принцип
, вывод и его применение
Эффект Холла
был введен американским физиком Эдвином Холлом в 1879 году. Он основан на измерении электромагнитного поля. Его также называют обычным эффектом Холла. Когда токопроводящий проводник перпендикулярен магнитному полю, генерируемое напряжение измеряется под прямым углом к пути тока. Где текущий поток аналогичен течению жидкости в трубе.Впервые он был применен при классификации химических образцов. Во-вторых, он был применим в датчике эффекта Холла, где он использовался для измерения полей постоянного тока магнита, где датчик остается неподвижным.
Принцип эффекта Холла
Эффект Холла определяется как разность напряжений, генерируемых на проводнике с током, поперек электрического тока в проводнике и приложенного магнитного поля, перпендикулярного току.
Эффект Холла = индуцированное электрическое поле / плотность тока * приложенное магнитное поле — (1)
эффект Холла
Теория эффекта Холла
Электрический ток определяется как поток заряженных частиц в проводящей среде.Текущие заряды могут быть либо отрицательно заряженными — электроны «e-», либо положительно заряженными — дырками «+».
Пример
Рассмотрим тонкую проводящую пластину длиной L и соединим оба конца пластины с батареей. Где один конец соединен с положительным концом батареи с одним концом пластины, а другой конец соединен с отрицательным концом батареи с другим концом пластины. Теперь мы наблюдаем, что в настоящее время начинает течь от отрицательного заряда к положительному концу пластины.Благодаря этому движению создается магнитное поле.
теория эффекта Холла
Сила Лоренца
Например, если мы разместим магнитную заглушку рядом с проводником, магнитное поле будет нарушать магнитное поле носителей заряда. Эта сила, искажающая направление носителей заряда, известна как сила Лоренца.
Благодаря этому электроны переместятся к одному концу пластины, а дырки переместятся к другому концу пластины. Здесь напряжение Холла измеряется мультиметром между двумя сторонами пластин.Этот эффект также известен как эффект Холла. Где ток прямо пропорционален отклоненным электронам, в свою очередь, пропорционален разности потенциалов между обеими пластинами.
Чем больше ток, тем больше отклоненные электроны и, следовательно, мы можем наблюдать большую разность потенциалов между пластинами.
Напряжение Холла прямо пропорционально электрическому току и приложенному магнитному полю.
VH = IB / qnd —– (2)
I — Ток, протекающий в датчике
B — Напряженность магнитного поля
q — Заряд
n — носителей заряда на единицу объема
d — Толщина датчика
Вывод коэффициента Холла
Пусть ток IX равен плотности тока, умноженной на JX на площадь коррекции проводника wt.
IX = JX wt = n q vx w t ———- (3)
Согласно закону Ома, если ток увеличивается, поле также увеличивается. Это дается как
JX = σ EX , ———— (4)
Где σ = проводимость материала в проводнике.
Рассматривая приведенный выше пример размещения магнитного стержня под прямым углом к проводнику, мы знаем, что на него действует сила Лоренца. При достижении устойчивого состояния не будет потока заряда в любом направлении, которое можно представить как:
EY = Vx Bz , ————– (5)
EY — электрическое поле / поле Холла в y-направление
Bz — магнитное поле в z-направлении
VH = — ∫0w EY day = — Ey w ———- (6)
VH = — ((1 / nq) IX Bz) / t , ———– (7)
Где RH = 1 / nq ———— (8)
Единицы эффекта Холла: m3 / C
Холловская подвижность
µ p или µ n = σ n RH ———— (9)
Холловская подвижность определяется как µ p или µ n — проводимость, обусловленная электронами и дырками.
Плотность магнитного потока
Она определяется как величина магнитного потока в области, взятой под прямым углом к направлению магнитного потока.
B = VH d / RH I ——– (1 0)
Эффект Холла в металлах и полупроводниках
В зависимости от электрического поля и магнитного поля носители заряда, движущиеся в среде, испытывают некоторое сопротивление из-за рассеяние между носителями и примесями, а также носителями и атомами материала, которые испытывают колебания.Следовательно, каждый носитель рассеивается и теряет свою энергию. Что можно представить следующим уравнением
-эффект Холла в металлах и полупроводниках
F retarded = — mv / t , ————– (1 1)
t = среднее время между рассеянием события
Согласно закону секунд Ньютона,
M (dv / dt) = (q (E + v * B) — mv) / t —— (1 2)
m = масса носителя
Когда наступает установившееся состояние, параметром ‘v’ пренебрегают
Если ‘B’ находится вдоль координаты z, мы можем получить набор уравнений ‘v’
vx = (qT Ex) / m + (qt BZ vy ) / м ———– (1 3)
vy = (qT Ey) / м — (qt BZ vx) / м ———— (1 4)
vz = qT Ez / м ———- (1 5)
Мы знаем, что Jx = nq vx ————— (1 6)
Подставляя в приведенные выше уравнения, мы можем изменить его как
Jx = (σ / (1 + (wc t) 2)) (Ex + wc t Ey) ———– (1 7)
Дж y = (σ * (Ey — wc t Ex) / (1 + (wc t) 2 ) ———- (1 8)
Jz = σ Ez ———— (1 9)
Мы знаем, что
σ n q2 т / м ———– (2 0)
σ = проводимость
t = время релаксации
и
wc q Bz / м ————– (2 1)
wc = циклотронная частота
Циклотронная частота определяется как частота вращения заряда в магнитном поле.Какая сила поля.
Что можно объяснить в следующих случаях, чтобы узнать, является ли он слабым и / или «t» коротким
Случай (i): Если wc t << 1
Указывает на ограничение слабого поля
Случай ( ii): Если wc t >> 1
Указывает на ограничение сильного поля.
Преимущества
К преимуществам эффекта Холла можно отнести следующее.
Скорость работы высокая, например 100 кГц
Цикл операций
Емкость для измерения большого тока
Может измерять нулевую скорость.
Недостатки
К недостаткам эффекта Холла можно отнести следующее.
Невозможно измерить поток тока, превышающий 10 см.
Температура сильно влияет на носители, которая прямо пропорциональна
Даже в отсутствие магнитного поля небольшое напряжение наблюдается, когда электроды находятся в центре.
Применения эффекта Холла
Применения эффекта Холла включают следующее.
No related posts.

принцип работы, теория, формула, применение

История эффекта Холла

Принцип работы эффекта Холла

Теория за принципом эффекта Холла

Формула эффекта Холла

Напряжение Холла

Коэффициент Холла

Концентрация несущей заряда

Холловская мобильности

Плотность магнитного потока

Применение принципа эффекта Холла

Как эффект Холла можно использовать для определения типа используемого полупроводника

Эффект Холла и его применение

В чем заключается эффект Холла

Аномальный ЭХ

Квантовый ЭХ

Спиновый ЭХ

Применение эффекта Холла

Что такое эффект Холла и где он применим?

Эффект Холла

Описание сути явления

Сущность эффекта Холла

Эффект холла и датчики на его основе

Эффект Холла.

История эффекта Холла

Теория за принципом эффекта Холла

Формула эффекта Холла

Напряжение Холла

Коэффициент Холла

Концентрация несущей заряда

Холловская мобильности

Плотность магнитного потока

Эффект Холла

Задача обучения

Основные пункты

Термины

Эффект холла — справочник студента

Узнай стоимость своей работы

Эффект Холла: в чём заключается явление, измерения датчиками, основанными на элементах Холла, формула расчетов

Открытие эффекта Холла

Узнай стоимость своей работы

Физико-математическое определение

Разновидности явления

Способы использования явления

Полупроводниковые материалы — Эффект Холла

Понятие и применение эффекта Холла

От Лоренца к Холлу

Использование эффекта Холла

Достоинства и недостатки

Изоляция

Синфазное напряжение

Теги

Применение эффекта Холла

Эффект Холла: принцип работы, теория, формула, применение

История эффекта Холла

Принцип работы эффекта Холла

Теория за принципом эффекта Холла

Формула эффекта Холла

Напряжение Холла

Коэффициент Холла

Концентрация несущей заряда

Холловская мобильности

Плотность магнитного потока

Применение принципа эффекта Холла

Как эффект Холла можно использовать для определения типа используемого полупроводника

11.7: Эффект Холла — Physics LibreTexts

Авторы и авторство

Эффект Холла | Физика

Цели обучения

Пример 1. Расчет ЭДС Холла: эффект Холла для кровотока

Сводка раздела

Концептуальные вопросы

Задачи и упражнения

Глоссарий

Избранные решения проблем и упражнения

2.1.3 Эффект Холла

Эффект Холла

Эффект Холла

Измерения эффекта Холла

Эффект Холла и сила Лоренца